|
n-мерные суммы.
Пирамида Хеопса сложена из камней. Вещество состоят из атомов. Живое состоит
из клеток. Все как-то и из чего-то складывается, преобразуется и
развивается. Камни разные, атомы разные, клетки – разные. А в сумме что-то
получается …
Хотя нет. Что-то развивается, а что-то вдруг
застывает в своем развитии.
Давайте, поиграем в кубики. Вон их сколько…,
выберем подходящие и начнем строить, … нет, сначала разложим, хотя бы по
размеру. Эти сюда, а эти…, нет, не подходят, каждый сам по себе, хотя бы пару им найти, тогда можно и в
дело. Ну вот, эту пару сюда, эту тут
приспособим…, эх, хватило бы …
А сколько должно быть? Что строить будем?
Вычислить количество сочетаний из n по k
элементов можно по формуле:
|
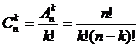
|
(1)
|
Числа 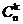 обычно называют
биномиальными коэффициентами. Отметим их простейшие свойства: обычно называют
биномиальными коэффициентами. Отметим их простейшие свойства:
Так как, по определению 0!=1, то:
|
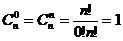
|
(2)
|
И далее:
|
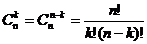
|
(3)
|
|
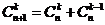
|
(4)
|
|
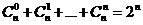
|
(5)
|
Интересно доказательство последнего свойства:
Из этого следует :
|
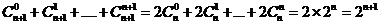
|
(7)
|
Что и
требовалось доказать. [1]
На этом
цитирование учебника можно бы
и закончить.
Ну вот, кое-какое теоретическое обоснование есть.
Теперь нам не составит труда вычислить количество сочетаний по k элементов из любого n элементов множества.
Например, найти количество сочетаний по 2 элемента
в группе из имеющихся, допустим, 7 элементов множества N. По формуле (1) находим:
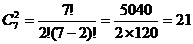
А, теперь, сочетания по 3 элемента из тех же 7:
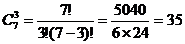
Остается спросить: А, что, собственно, мы
получили?
Количество. Но, из чего оно складывается?
Например, по 2 из 7.
Чтобы это узнать, возьмем в руки ручку и начнем
составлять эти пары, количество-то их мы уже знаем. 1,2; 1,3; 1,4; … 2,3;
... 3,4; … 6,7; Все.
Действительно, 21 пара. С цифры 1 начинается 6
пар, с 2 начинается 5 пар, ну, и т.д. И одна пара: 6,7; Так мы их и
сосчитаем:
6+5+4+3+2+1 = 21.
Таким образом:
|
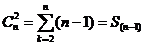
|
(8)
|
Где 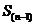 , это сумма чисел натурального ряда от 1 до (n-1). , это сумма чисел натурального ряда от 1 до (n-1).
Теперь проделаем ту же операцию с сочетаниями по 3
из 7.
1,2,3; 1,2,4; … 1,2,7; 1,3,4; … 1,6,7; 2,3,4;
2,3,5; … 5,6,7;
Всего 35 сочетаний. Мы их тоже сосчитаем:
|
5+4+3+2+1+
4+3+2+1+
3+2+1+
2+1+
1= 35
|
Естественно, вместо записи в одну строку, я
расположил суммируемые цифры так, что бы было видно получаемую картинку.
Красиво получилось. Вот только написать формулу для этого действия будет
затруднительно.
Мы развернули суммируемые числа на плоскости. В
прямоугольных координатах. На осях расположились отрезки натурального ряда
1,2,3,4,5. Во всех остальных направлениях между осями полного набора чисел
нет. Если провести аналогию с измерением площади квадрата, где S = a2 , то можно
записать получаемую нами сумму сочетаний
по 3 из 7 в таком виде:
|
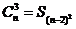
|
(9)
|
Вот теперь мы можем составить формулу получения
количества сочетаний по k из n способом
суммирования для любых сочетаний:
|
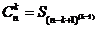
|
(10)
|
Понятно, что в данном случае степень (k-1)
показывает только количество координатных осей пространства на плоскости, на которых
разворачиваются полные отрезки
натурального ряда. Но, не степень числа, в принятом понимании….
Разворот суммы идет на плоскости.
Это надо показать.
Для упрощения рисунка мы опустим в нем знаки
суммирования. Мы же все равно помним, что все эти числа – слагаемые. Как бы
они не располагались в пространстве, их все равно надо сложить все. И получить
результат – число сочетаний.
Вернемся к двухмерной сумме. Она, как мы помним, в
прямоугольном координатном пространстве выглядит вот так:
|
1
|
|
|
|
|
|
|
|
2
|
1
|
|
|
|
|
|
|
3
|
2
|
1
|
|
|
|
|
|
4
|
3
|
2
|
1
|
|
|
|
|
5
|
4
|
3
|
2
|
1
|
|
|
|
6
|
5
|
4
|
3
|
2
|
1
|
|
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
Рис.1 Двухмерная пространственная
сумма.
Цветом выделены
направления пространственных осей.
Теперь посмотрим, как будет выглядеть трехмерная
сумма. Она имеет два варианта расположения:
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
2
|
1
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
3
|
2
|
1
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
4
|
3
|
2
|
1
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
5
|
4
|
3
|
2
|
1
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
Рис.2. Трехмерная
пространственная сумма. Вариант 1.
Это продолжение разворота по аналогии к
предыдущему рис.1. Второй вариант, как мне кажется, более компактен.
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
2
|
2
|
2
|
2
|
2
|
1
|
|
3
|
3
|
3
|
3
|
3
|
2
|
1
|
|
4
|
4
|
4
|
4
|
3
|
2
|
1
|
|
5
|
5
|
5
|
4
|
3
|
2
|
1
|
|
6
|
6
|
5
|
4
|
3
|
2
|
1
|
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
Рис.3. Трехмерная
пространственная сумма. Вариант 2.
В качестве третьей оси используется направление
диагонали квадрата. Но, результат суммирования чисел трехмерной суммы,
очевидно, будет одинаков в любом случае.
Эти варианты форм представления стали основой для построения
треугольника Паскаля и прямоугольника Тарталья [2].
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
2
|
1
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
3
|
2
|
1
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
4
|
3
|
2
|
1
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
5
|
4
|
3
|
2
|
1
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
Рис.4. 4-мерная открытая пространственная сумма.
С четырехмерной суммой проблем так же не
возникает.
Мы достраиваем очередной участок плоскости
сложения и получаем, например, такую картинку, как на рис. 4.
А сейчас, проверим правильность применения n-мерных сумм в расчетах количества сочетаний.
На одном из
свойств 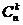 . .
Например,
свойство (5): 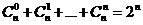
Примем n=5 и k =
0…5. Результаты вычислений сведены в
таблицу1.
Таблица 1
|
Биномиальные
коэффициенты
|
n-мерные суммы
|
|
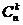
|
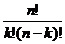
|
Результат
|
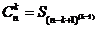
|
Форма
представления
|
Результат
|
|
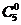
|
120/0
|
1
|
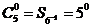
|
1
|
1
|
|
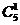
|
120/1*24
|
5
|
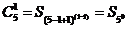
|
1+1+1+1+1
|
5
|
|
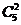
|
120/2*6
|
10
|
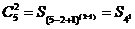
|
|
10
|
|
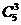
|
120/6*2
|
10
|
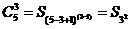
|
|
10
|
|
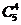
|
120/24*1
|
5
|
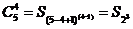
|
|
5
|
|
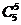
|
120/120
|
1
|
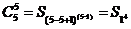
|
1
|
1
|
Вычисление 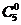 по свойству (2) в обоих случаях основано
на соглашениях. Есть соглашение, что в сочетании по 0 чисел в каждой группе
должен получиться результат 1. С
этого начинаются свойства биномиальных коэффициентов (2). В n-мерных суммах
число в основании указывает количество слагаемых из первых чисел
натурального ряда на
пространственных осях. Формула (10)
в этом случае дает отрицательную координату пространства. Это и говорит об
отсутствии слагаемых в сумме. Нет ни оси, ни слагаемых. Соглашаемся на единичный результат. по свойству (2) в обоих случаях основано
на соглашениях. Есть соглашение, что в сочетании по 0 чисел в каждой группе
должен получиться результат 1. С
этого начинаются свойства биномиальных коэффициентов (2). В n-мерных суммах
число в основании указывает количество слагаемых из первых чисел
натурального ряда на
пространственных осях. Формула (10)
в этом случае дает отрицательную координату пространства. Это и говорит об
отсутствии слагаемых в сумме. Нет ни оси, ни слагаемых. Соглашаемся на единичный результат.
При подсчете количества сочетаний по одному
элементу в группе формальной пространственной оси в пространстве сложения
нет. Есть отдельные точки, в количестве равным n. Так и
получилось при расчете по формуле (10).
А дальше, как мы видим, результаты совпадают. И
результат вычислений соответствует свойству (5) и следствию (7). Теперь проверим свойство (4). Для
примера возьмем:
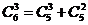
В виде n-мерных
сумм такое выражение выглядит вот так:
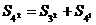
Что соответствует вот такому, как на рис.5.
сложению форм представления:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
3
|
2
|
1
|
|
|
|
|
|
|
|
|
3
|
2
|
1
|
|
|
|
3
|
2
|
1
|
|
|
4
|
3
|
2
|
1
|
|
+
|
|
2
|
1
|
|
|
=
|
|
2
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
1
|
|
|
|
Рис.5. Сложение n-мерных сумм в формах представления.
Как мне кажется, выглядит достаточно
показательно. Но, к сожалению, так
просто и красиво получается не всегда.
Возьмем классический треугольник Паскаля.
Например, из [2]. Он на рис.6.
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
2
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
3
|
|
3
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
4
|
|
6
|
|
4
|
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
5
|
|
10
|
|
10
|
|
5
|
|
1
|
|
|
|
|
|
|
|
|
1
|
|
6
|
|
15
|
|
20
|
|
15
|
|
6
|
|
1
|
|
|
|
|
|
|
1
|
|
7
|
|
21
|
|
35
|
|
35
|
|
21
|
|
7
|
|
1
|
|
|
|
|
1
|
|
8
|
|
28
|
|
56
|
|
70
|
|
56
|
|
28
|
|
8
|
|
1
|
|
|
1
|
|
9
|
|
36
|
|
84
|
|
126
|
|
126
|
|
84
|
|
36
|
|
9
|
|
1
|
Рис.6. Треугольник
Паскаля.
Немного его доработаем, сдвинем вершину и
уплотним. Вид его несколько изменился, но содержание осталось прежним. Он
все так же отражает биномиальные коэффициенты. Я выделил тот пример, на
котором мы рассчитывали n-мерные
суммы, приведенные в табл.1. На нем
стало понятно, как пользоваться данными таблицы 2. Для удобства в таблицу введено обобщенное
выражение n-мерной суммы:
|
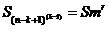
|
(11)
|
Где m = (n-k+1), r = (k-1)
Таблица 2.
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
k
|
2n
|
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
1
|
1
|
1
|
|
|
|
|
|
|
|
|
|
2
|
|
2
|
1
|
2
|
1
|
|
|
|
|
|
|
|
|
4
|
|
3
|
1
|
3
|
3
|
1
|
|
|
|
|
|
|
|
8
|
|
4
|
1
|
4
|
6
|
4
|
1
|
|
|
|
|
|
|
16
|
|
5
|
1
|
5
|
10
|
10
|
5
|
1
|
|
|
|
|
|
32
|
|
6
|
1
|
6
|
15
|
20
|
15
|
6
|
1
|
|
|
|
|
64
|
|
7
|
1
|
7
|
21
|
35
|
35
|
21
|
7
|
1
|
|
|
|
128
|
|
8
|
1
|
8
|
28
|
56
|
70
|
56
|
28
|
8
|
1
|
|
|
256
|
|
9
|
1
|
9
|
36
|
84
|
126
|
126
|
84
|
36
|
9
|
1
|
|
512
|
|
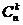
|
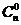
|
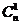
|
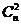
|
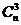
|
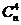
|
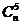
|
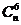
|
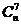
|
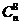
|
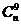
|
|
|
|
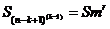
|
S0m
|
Sm0
|
Sm1
|
Sm2
|
Sm3
|
Sm4
|
Sm5
|
Sm6
|
Sm7
|
Sm8
|
|
|
На пересечении строки выбранного n и столбца значения k в пределах треугольника Паскаля определяются количества сочетаний или
биномиальные коэффициенты, и соответствующие им n-мерные суммы.
Рассматривая n-мерные суммы, мы обращались к количеству
сочетаний объектов. Действительно,
сумма дает количественную оценку. Количество чего? Например, мы говорим,
что площадь квадрата составляет S = a2 . В
данном случае мы говорим о количестве каких-то единиц пространства,
составляющих измеряемый нами объект. И формула V=a3, для измерения объема говорит о том же. Только
единицы эти различны. В первом случае это единичные квадратики, а во втором
– кубики. В этом смысле математическое действие умножение задает единицы
измерения. В первом случае это - а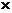 а, а во втором - а а, а во втором - а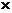 а а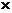 а. Сложение не меняет с такой легкостью единицы измерения
результата. Оно вообще не
меняет пространственной составляющей
единиц. а. Сложение не меняет с такой легкостью единицы измерения
результата. Оно вообще не
меняет пространственной составляющей
единиц.
В наших примерах, сложение использует единицы
измерения пространства, заданные условиями задачи. Это, когда размерность
единиц задана, если же нет, то – кубики, шарики и т.д., - единицы объема.
Мы живем в объеме, и общими для всех будут видимо его единицы.
Сочетания не учитывают порядок следования
объектов. И потому, при подсчете сочетаний, например по 2 из 4, такие
сочетания как 12 и 21, нам придется
объединить в одно. Из 16 возможных
сочетаний у нас останется только 6. Остальные
придется отбросить по различным причинам.
Вот он наш выбор, на рис.8.
|
|
1
|
2
|
3
|
4
|
|
1
|
|
|
|
|
|
2
|
21
|
|
|
|
|
3
|
31
|
32
|
|
|
|
4
|
41
|
42
|
43
|
|
Рис. 8. Сочетания из 4 по 2.
Результат, как выражение суммы слагаемых мы
запишем как 3+2+1 =6. Интересно, выбираем из единиц площади, а получаем –
линейную одномерную запись выражения суммы.
То, что отражено на рис.8. лишь графический
портрет, а реальные единицы должны иметь объем. Например, как на рис.9.
Рис.9. Объекты счета в
сочетаниях по 2 из 4.
Мы считаем сочетания пар, а … играем в кубики. Ну,
конечно, единицы счета сочетаний
отражают лишь факт выбора абстрактной единицы, как эквивалента выбранной
пары. Реальные объекты могут не беспокоиться …, в моделях n-мерных сумм сами они пока не участвуют.
Увеличение размерности суммы не приводит к
изменению пространственных характеристик единиц измерения. Кубики позволяют
показать пространственные модели n-мерных
сумм до 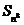 . Дальнейшее увеличение n-мерности не позволит прямоугольная система
координат. . Дальнейшее увеличение n-мерности не позволит прямоугольная система
координат.
Вот так (рис.10) выглядит модель 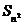 , как количество счетных единиц. , как количество счетных единиц.
Рис.10. Модель суммы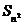 . .
И тут, при учете реального количества счетных
единиц добавляется еще одна пространственная ось. В числах эта же сумма на
рис.1. Мы выбирали сочетания по 3
элемента из n возможных.
Теперь понятно, что отражают рис.2-4. Это площадь, под объемной моделью,
отражающей реальное количество возможных сочетаний. План ее расположения.
Объемная модель математической n-мерной суммы, как
оказалось, вполне определенный
геометрический объект. И теперь понятие n-мерной суммы может быть расширено с этих позиций
уже до самостоятельного способа построения пространственных тел. При этом ее связь с биномиальными коэффициентами становится только
частным случаем формирования n-мерной
суммы.
В чем различие двух записей одной и той же
суммы: S=1+2+3…
и S=3+2+1 ?
В возможности продолжения записи. В первом случае
это возможно, а во втором – нет. В линейной сумме это не так заметно, а вот
уже в 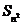 отличия видны
отчетливо. отличия видны
отчетливо.

Рис.6. Открытая и закрытая сумма.
На рис.6. вариант а)
отражает сумму сочетаний по 3 из 6.
А что отражает вариант б)?
Конкретно
эта сумма, если складывать вертикали, отражает сумму квадратов чисел
натурального ряда. Но, построений сумм много, и общей формулы пока нет, или
мне это пока неизвестно. Могу
сказать лишь то, что при таком расположении слагаемых суммы, в отличии от а)., она
всегда может быть расширена. Этот вариант открыт для дополнения.
Вариант а) измениться уже не может. Это закрытая сумма.
Суммы а) и б) по сути записи
являются противоположностями.
При увеличении n-мерности суммы, независимо от варианта
построения, количество осей пространства суммирования на одну больше, чем
количество заполненных межосевых участков. И это положение сохраняется при
любом количестве осей. Пространство суммирования останется незамкнутым
вокруг начала координат, пока мы его не замкнем принудительно. Замкнутая
пространственная сумма, обозначим ее как Sz, может быть получена так:
|
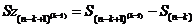
|
(12)
|
Для этого необходимо убрать одну из краевых осевых
линейных сумм. Пространство суммирования замкнется. Но, такая сумма уже не
будет соответствовать каким-либо сочетаниям по k из n. Это уже
самостоятельный объект. Чтобы сохранить простоту и линейность на рис.7. я
показал простейший вариант замкнутой n-мерной суммы. До замыкания эта сумма имела 5 пространственных
осей. После замыкания осталось 4.
|
|
|
1
|
|
|
|
|
1
|
2
|
1
|
|
|
1
|
2
|
3
|
2
|
1
|
|
|
1
|
2
|
1
|
|
|
|
|
1
|
|
|
Рис.7. Замкнутая n-мерная сумма.
Замыкая n-мерную
сумму, мы ограничиваем ее размерность. И дальнейшее увеличение размерности
этой суммы становится невозможным. Замыкание
суммы возможно при ее размерности 2 и более. Одномерную, линейную сумму
типа Sn=3+2+1 замкнуть, видимо не удастся.
При замыкании суммы мы создаем из нее замкнутый пространственный объект.
Координатные оси становятся осями
симметрии. Если сумма открытая, то она может развиваться дальше в созданной
системе симметрий. Если сумма была закрытой, то развитие останавливается на
достигнутом уровне.
n-мерные суммы с основанием Ф.
Все предыдущие построения мы производили, имея в основе суммы чисел натурального
ряда. В основании этого ряда – счетная единица. Для перехода на другое основание счета
воспользуемся формулой бинома
Ньютона.
Один из вариантов представления бинома Ньютона:
|
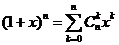
|
(13)
|
Если 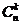 заменить на: заменить на:
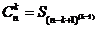
Формула бинома Ньютона приобретет вид:
|
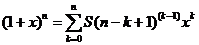
|
(14)
|
Теперь произведем
еще одну замену. Ну, конечно:
х =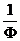
И формула
становится такой:
|
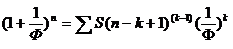
|
(15)
|
Еще одно преобразование:
|
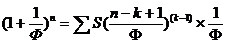
|
(16)
|
Теперь вернемся к данным таблицы 1 и продолжим расчеты по формуле (15).
Все полученные расчетные данные сводим в таблицу
3.
Таблица 3.
|
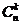
|
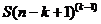
|
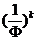
|
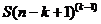 * *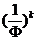
|
|
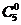
|
1
|
1
|
1
|
|
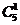
|
5
|
0,618…
|
3,09
|
|
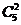
|
10
|
0,382
|
3,82
|
|
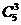
|
10
|
0,236
|
2,36
|
|
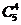
|
5
|
0,146
|
0,73
|
|
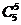
|
1
|
0,09
|
0,09
|
Эти данные пока невозможно представить в виде
целочисленной n-мерной суммы. Они нужны для
последующего преобразования и
приведения к числам Люка и Фибоначчи.
По форме похоже на треугольник Паскаля.
Треугольник Паскаля и взят за основу построения
таблицы 4. В нем данные до n=9 и k=9 пересчитаны по формуле (15). Вот что
получилось:
Таблица 4.
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
k
|
Фn
|
|
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
1
|
1
|
0,62
|
|
|
|
|
|
|
|
|
|
1,62
|
|
|
2
|
1
|
1,24
|
0,382
|
|
|
|
|
|
|
|
|
2,62
|
|
|
3
|
1
|
1,85
|
1,146
|
0,24
|
|
|
|
|
|
|
|
4,236
|
|
|
4
|
1
|
2,47
|
2,29
|
0,94
|
0,15
|
|
|
|
|
|
|
6,85
|
|
|
5
|
1
|
3,09
|
3,82
|
2,36
|
0,73
|
0,09
|
|
|
|
|
|
11,09
|
|
|
6
|
1
|
3,7
|
5,73
|
4,72
|
2,19
|
0,54
|
0,1
|
|
|
|
|
17,93
|
|
|
7
|
1
|
4,24
|
8,02
|
8,26
|
5,11
|
1,89
|
0,4
|
0,03
|
|
|
|
28,95
|
|
|
8
|
1
|
4,94
|
10,7
|
13,22
|
10,2
|
5,04
|
1,6
|
0,27
|
0,02
|
|
|
46,98
|
|
|
9
|
1
|
5,56
|
13,75
|
19,82
|
18,4
|
11,34
|
4,7
|
1,22
|
0,2
|
0,013
|
|
76,005
|
|
|
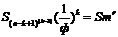
|
S0m
|
Sm0
|
Sm1
|
Sm2
|
Sm3
|
Sm4
|
Sm5
|
Sm6
|
Sm7
|
Sm8
|
|
|
|
|
Переведем результаты в целочисленную форму. Для
этого необходимо округлить полученные данные до целочисленных значений.
Получилась таблица 5.
Так выглядит треугольник, приведенный к числам Люка. На ровный треугольник это не
совсем похоже. Но, система
построения уже видна. Некоторые округления в целях сохранения общего
результата пришлось сделать с нарушением правил округления. Таких чисел
немного.
Таблица 5
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
k
|
Числа
Люка
|
|
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
2
|
1
|
1
|
1
|
|
|
|
|
|
|
|
|
3
|
|
|
3
|
1
|
2
|
1
|
|
|
|
|
|
|
|
|
4
|
|
|
4
|
1
|
3
|
2
|
1
|
|
|
|
|
|
|
|
7
|
|
|
5
|
1
|
3
|
4
|
2
|
1
|
|
|
|
|
|
|
11
|
|
|
6
|
1
|
4
|
6
|
5
|
2
|
0
|
|
|
|
|
|
18
|
|
|
7
|
1
|
4
|
8
|
8
|
5
|
2
|
1
|
|
|
|
|
29
|
|
|
8
|
1
|
5
|
11
|
13
|
10
|
5
|
2
|
|
|
|
|
47
|
|
|
9
|
1
|
6
|
14
|
20
|
18
|
11
|
5
|
1
|
|
|
|
76
|
|
|
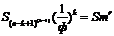
|
S0m
|
Sm0
|
Sm1
|
Sm2
|
Sm3
|
Sm4
|
Sm5
|
Sm6
|
Sm7
|
Sm8
|
|
|
|
|
Вполне возможно, что данные полученного
треугольника будут позже немного скорректированы.
Приведение первичных данных к числам Фибоначчи
потребовало значительной коррекции. Наиболее устойчивая форма отражена в
таблице 6. Возможно, она также претерпит дальнейшие изменения, но пока -
так.
Таблица 6
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
k
|
Числа
Фибоначчи
|
|
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
1
|
1
|
1
|
|
|
|
|
|
|
|
|
|
2
|
|
|
2
|
1
|
1
|
1
|
|
|
|
|
|
|
|
|
3
|
|
|
3
|
1
|
2
|
1
|
1
|
|
|
|
|
|
|
|
5
|
|
|
4
|
1
|
3
|
2
|
1
|
1
|
|
|
|
|
|
|
8
|
|
|
5
|
1
|
3
|
4
|
3
|
1
|
1
|
|
|
|
|
|
13
|
|
|
6
|
1
|
4
|
6
|
5
|
3
|
1
|
1
|
|
|
|
|
21
|
|
|
7
|
1
|
5
|
8
|
9
|
6
|
3
|
1
|
1
|
|
|
|
34
|
|
|
8
|
1
|
6
|
12
|
14
|
12
|
6
|
2
|
1
|
1
|
|
|
55
|
|
|
9
|
1
|
7
|
15
|
22
|
20
|
14
|
6
|
2
|
1
|
1
|
|
89
|
|
|
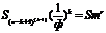
|
S0m
|
Sm0
|
Sm1
|
Sm2
|
Sm3
|
Sm4
|
Sm5
|
Sm6
|
Sm7
|
Sm8
|
|
|
|
|
Я пока не знаю, как достоверно интерпретировать
полученные результаты. Например, вернемся к уже знакомому примеру:
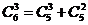
В виде n-мерных
сумм такое выражение выглядит вот так:
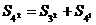
Данные возьмем из таблиц 5 и 6, теперь попробуем
установить формы представления n-мерной
суммы. Результаты в таблице 7.
Таблица 7.
|
Сумма
|
Возможная
форма представления
|
|
|
|
|
S32=3(F)
|
|
|
S32= 2(L)
|
|
|
|
|
|
S4 =4(F)
|
|
Как мы видим, результаты не соответствуют уже привычным формам.
Чем отличаются основание 1 от основания Ф? Как
понимать это в геометрическом представлении и что должно измениться
с введением нового основания?
Единичный объем, это и объем клетки, и объем кроны огромного дерева. Вот этого
– единственного. Единичность,
понятие относительное. Она привязана к основанию счетной системы и единицам
ее измерения. И тут далеко не все равно, в чем измерять, в «мартышках» или
«попугаях». В каждом случае получится своя единичность. И они не сравнимы.
Для сравнения необходимо общее основание счета. И потому, все приведенные
ниже примеры, это определенный компромисс. Единичность мы получаем в
счетных единицах, а основанием счета пытаемся ввести Ф. Примем, что 1= Ф0. На этом и остановимся. И забудем о
соотношениях объемов. В данном случае они сравниваться не могут.
Тогда, возможно, должна соответственно измениться
форма объема новой единицы, как эквивалента основания. Что такое единичный
объем – понятно, вот на рис.8. варианты получения объема, близкого к 1, с
использованием основания Ф.

Рис. 8. Примеры получения объема 1,0
а) эллипсоид
вращения, в) призма и с) шар.
Я обращаю внимание даже не на близость к
единичному значению, а на идентичность результата.
Объем шара:
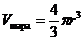
Где r = 0,618… ; r3=0,2360679…;
Vшара=4/3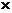 3,14159265359… 3,14159265359…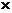 0,236067…=0,98883923181… 0,236067…=0,98883923181…
Объем эллипсоида вращения:
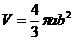
Где a=1,618…; и b=0,381966…;
b2=0,145898…
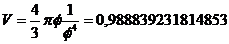
Как мы видим, при приведении этих двух различных
формул к основанию Ф они становятся одной формулой.
Кстати, параболоид вращения, а также гиперболоид
тоже могут иметь такие соотношения высоты и радиуса наибольшего диаметра вращения при объеме очень
близком к 1. Объем параболоида вращения:
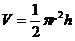
Если принять, что r = 1/ф, и h = ф, то формула
превратится в:
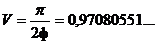
Приближение к тому же единичному объему.
Простота получения сложной кривизны шокирует.
Остается только менять коэффициенты при постоянной величине 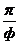 и получать любые
вариации формообразования. и получать любые
вариации формообразования.
Если формулы получения объема шара, эллипсоида и
параболоида вращения попробовать объединить в одну, на основе Ф, то мы
получим:
|
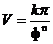
|
(17)
|
Формула содержит три основных составляющих:
соотношение k в счетных единицах и две
константы, определяющие формообразование. Уберите любую составляющую, и
форма объема изменится соответствующим образом.
Дальше все как старой загадке: Столько, да
полстолька, да четверть столько, да еще один…, так и получим любую степень
основания Ф элементарным сложением. Счетная система Бергмана у природы явно
в большом почете. Вот где появляются реальные многомерные суммы,
позволяющие создавать объемы сложных форм.
Но, использовать константу 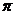 , это еще не значит создавать только шары и круги. Это значит создавать замкнутый
объем плавным изменением кривизны поверхности. И оказывается, что
эллипсоиды, параболоиды и гиперболоиды строить проще. Строим, куда кривая
выведет, главное – плавно завершить.
И чтобы по возможности прочно,
надежно, с прицелом на
дальнейшее развитие. На жесткий контроль всего строительства в целом, как того требует сфера, нет ни
времени, ни средств. Шарообразные
объемы, создаваемые природой, при всем их многообразии, все же только
частный случай и почти всегда весьма приблизительный. Общими являются, как
раз, большие отклонения от сферы. На всех уровнях формообразования. От
клеток до деревьев или человека. , это еще не значит создавать только шары и круги. Это значит создавать замкнутый
объем плавным изменением кривизны поверхности. И оказывается, что
эллипсоиды, параболоиды и гиперболоиды строить проще. Строим, куда кривая
выведет, главное – плавно завершить.
И чтобы по возможности прочно,
надежно, с прицелом на
дальнейшее развитие. На жесткий контроль всего строительства в целом, как того требует сфера, нет ни
времени, ни средств. Шарообразные
объемы, создаваемые природой, при всем их многообразии, все же только
частный случай и почти всегда весьма приблизительный. Общими являются, как
раз, большие отклонения от сферы. На всех уровнях формообразования. От
клеток до деревьев или человека.
Но, начинают клетки. Это строительные кирпичики
всего остального, относящегося к Живому. Геометрия клетки косвенно
определяет геометрию построенной из таких клеток структуры. Как мне
кажется, любые отклонения от сферы в конечном итоге доводятся до
соотношений, оптимальных для строительства единой структуры из единичных
объемов. В том числе и до показанных выше. При
этом обеспечивается наибольшая плотность элементов с сохранением
максимального разнообразия
формообразования. Видимо, реальные n-мерные суммы в объемном варианте строятся
примерно из таких элементов. Как мне кажется, здесь и начинается
филлотаксис…
Мы все
время говорим то о математических сочетаниях, то об элементах многомерной
суммы. Теория вероятностей считает
количество эквивалентов суммы признаков отбора по заданным условиям. И
каждый вроде бы всего лишь счетный эквивалент вдруг становится реальным
объектом. Таким же реальным, как и первичные, для которых мы считали
количество сочетаний.
Я
рассматривал пространственные модели
суммы и вдруг сделал простой вывод – появляющиеся
в модели единицы количества сочетаний несут в себе признаки прошлого
отбора и, одновременно сами
могут стать частью основы для выбора новых допустимых сочетаний.
Вместе с
первичным множеством. Складываем первичное множество и результат отбора, и
получаем новое множество с новой возможностью отбора допустимых сочетаний. По тем же законам.
Или уже по другим. Это зависит от заданных условий прогрессивного отбора.
Первый уровень отбора уже пройден. Новое полученное множество свободно от
прошлых условий и пригодно для любого нового отбора сочетаний.
Многоуровневая система отбора сочетаний из суммы
первичного множества и результатов прошлых отборов приводит к бесконечному
росту количества сочетаний. Это и есть прогрессия.
Формула
(1) дает количественную оценку сочетаний без учета уровня. Все и сразу. Для
получения реального количества
сочетаний, возникших на данном уровне отбора необходимо вычесть из
полученного результата вычислений по формуле (1) количество сочетаний
прошлых уровней.
Прогрессия
суммы высветила очень важный момент в отборе сочетаний. Каждый элемент
множества может иметь признаки прошлого отбора. Он связан с прошлым
множеством информацией отбора. На новом уровне множество изменилось, но …
связи остались. Причинно-следственные связи. Что было до того, после того и
вместо того, что стало сейчас. Каждая единица из общего количества вдруг
обрела индивидуальность.
С чего мы
начинали? С простых счетных единиц. Это были просто нумерованные однотипные
объекты, которые от уровня к уровню вдруг стали приобретать
индивидуальность признаков. Система связей между уровнями отбора вдруг
обрела самодостаточность. Стало необходимым учитывать не только количество
сочетаний, но и их связи. Все, прошлые и настоящие. Эти связи стали основным условием отбора
сочетаний из множества.
С другой
стороны, рост количества
сочетаний, как реальных объектов,
в том числе и счета, в составе n-мерной суммы, в пространстве суммирования, это, в конечном итоге -
формообразование. И суммы,
и ее составляющих. Мы строим форму из производных от первичного множества и
самого множества. Эти элементы математически неразличимы. Осталось сделать
их такими в реальности. Одинаковыми, как кирпичи.
И строить…
Отбор
сочетаний по правилам теории вероятностей, это только математический прием
генерации счетных эквивалентов.
Хорошо проверяемый, но все же - частный случай. Но,
кирпичики появились. И уже не важно,
как именно, важно, что у них есть форма, объем, и из них можно
сделать что-то ...
Март 2007
г.
г.
Екатеринбург
1.
И.А.Палий. Введение в теорию вероятностей: Учебное
пособие. -М. :Высшая Школа, 2005. – 175 стр.
2.
А.П.Стахов. Новый
тип элементарной математики и компьютерной науки, основанной на «золотом
сечении». Винница 2003г.
|