|
Хаос, фракталы, аттракторы,
как всё это странным образом пересекается на простейшем, в общем,
уравнении. С него начался целый класс разностных уравнений:
«Одномерное отображение с одним квадратичным максимумом
вида:
xn+1=λxn(1–xn) (П2.1)
было введено в 1845г. П.Ф. Ферхюльстом
для описания динамики изменения численности особей одного вида в замкнутой
среде».[9]
«Всплеск интереса к разностному уравнению произошел в 1978 г., после того, как
американский ученый М. Фейгенбаум установил с его
помощью наличие универсальных закономерностей перехода к хаосу через
последовательность бифуркаций удвоения периода. Фейгенбаум
показал, что эти закономерности присущи всем отображениям вида xn+1=f(xn), в которых функция f(xn) на интервале рассмотрения имеет
единственный квадратичный максимум, а качественное поведение при переходе к
хаосу описывается универсальными константами (называемых константами Фейгенбаума α и δ)» [9].
α=2.5029078750…
δ=4.669201…
Так, для памяти…
Получается, что это уравнение
осмысливают и решают уже более полутора веков, а оно все еще манит и манит
к себе новых исследователей. Вроде и загадок в нем давно уже нет, а вот …
ищут же чего-то?
Конечно, сначала удивляет вид
графика, получаемого в результате отражения результатов вычисления на
координатной плоскости. Фрактальное образование. График расходится на
ветви, которые продолжают множиться и расходиться, всё это превращается в
дерево с густой кроной … хаоса. Вот изображение этого дерева, на рис.1.:

Рис.1.
Дерево фрактала.
Похожую картинку на рис.2 дает
А.Никифоров [2].
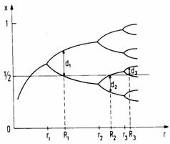
Рис.2. График из статьи А.Никифорова.
Как мы видим, А.Никифоров [2] не рассматривает переход к хаосу,
ограничиваясь фракталами. Видимо,
далее уже трудно разобраться…
В российских статьях на эту
тему уравнение Фейгенбаума часто имеет вид:
Отличие небольшое. И потому
далее мы будем говорить о формуле в этом, может быть, более привычном для
нас виде.
Есть в построении графика логистического уравнения некоторая тонкость. Если
каждое новое вычисление xn приносит новый результат, который в линейную функцию не
укладывается и остается только точкой на общем графике, то это и есть итерация
- получение каждого нового значения последовательности xn только
вычислением.
Можно это же выражение
записать и как:
Затем взять некоторое
начальное значение x и
начать вычисления с каким-то шагом изменения С, а полученные соседние точки,
допустим, соединять линией, то … мы получим кривую, напоминающую синусоиду,
плавно увеличивающую размах колебаний от Ymax до Ymin,
с фиксацией все большего количества точек с увеличением С. Причем, при каком-то увеличении С количество расчетных точек кривой
на отрезке от Ymax до Ymin будет
увеличиваться. 2;4;8; и т.д.
Но,… точки полученного графика
соединить линией промежуточных
функциональных значений не удается. Разрыв всегда остается. Это и есть бифуркация.
И как мы уже говорили, количество бифуркации все время увеличивается. С
этих позиций уравнение рассматривается как бифуркации с периодом 2 в
функции типа xn+1 = f(xn).
Функция есть, и … построение
линейного графика изменения переменной невозможно. Одни бифуркации…, точки
в области определения этой функции…
Если не знать нужного
диапазона изменения С, в котором отмечается
найденное удвоение бифуркаций, то его надо будет еще поискать, и достаточно
долго. Пока, как утверждается во многих публикациях, это узкая полоска,
примерно, 3,54<C<3,57, между прочим…
Вернемся к итерациям и формуле
последовательности (1). При заданном Х1
и С = const
все точки полученных результатов будут размещаться на одной вертикали. Но,
если задать достаточно малый шаг изменения С и повторить расчеты, то
точки результатов вычислений сами образуют линии близких значений, которые
выстроятся в разветвляющуюся структуру, в которой каждый новый уровень
ветвей повторяет предыдущий, но в другом масштабе. Это фрактальная структура с шагом
2.
Чем меньше шаг изменения С и больше заданное количество n, тем точнее мы получим картинку структуры этого
графика.
Это маленькое пояснение позволяет немного понять, о чем говорят
авторы многочисленных публикаций на тему логистического
уравнения Фейгенбаума. Например, С.В.Поршнев [7]
говорит о бифуркациях функции xn+1 = f(xn), а сам М.Фейгенбаум,
говоря об этом уравнении, рассказывает об итерациях и фракталах. Они
говорят об одном и том же, но с разных сторон математики.
Таким образом, для получения
более или менее полной графической картинки для данного уравнения надо
задать количество итераций при С=const (количество результатов по
вертикали), а потом задать количество значений С в заданном диапазоне его
изменения (количество значений по горизонтали). Посчитаем такой двойной
цикл … и получим картинку распределения точек результатов вычислений в
прямоугольных координатах по заданным диапазонам изменения Х и С. Так,
например, получен график на рис.1.
Как утверждают все
исследователи, точность получения четкой фрактальной структуры на основе
данного логистического уравнения ограничена
вычислительными возможностями компьютера.
Если погрешность вычисления сильно влияет на результат очередной
итерации, то … новый полученный результат уже не отражает реальной картины
и равновероятно может попасть в любую точку плоскости отражения графика.
Видимо с этого момента стройная картинка фракталов переходит в картинку
случайной вероятности.
Вот, например, такое описание:
«…В
области 1<с<3 значение Х приближается
к ненулевому постоянному значению
X*=1-1/c
, определяемому
подстановкой в уравнение вместо Xj+1 и Xj их предела X* . Это
область стационарных решений.
…При
3<c<3,4
появляются уже две ветви кривой.
…Далее,
при 3,4<с<3,54 имеются
уже четыре ветви. Возникает четырехстадийный цикл
колебания. Период цикла удваивается. Затем появляются 8, 16, 32, ...
, ,2n ветвей.
…При
значении С беск=3,57 движение
становится апериодическим (период цикла стремится к бесконечности). Начиная С=Сбеск,
поведение системы приобретает хаотический характер. Происходит перекрытие
областей различных решений. Динамические переменные Xj
принимают значения, которые сильно зависят от начальных.
При расчетах на ЭВМ для близких начальных значений решения уравнения могут
резко различаться. Точность ЭВМ уже становится недостаточной, расчеты —
некорректными. Они начинают зависеть от случайных процессов в самой ЭВМ».[ ]
Формула Фейгенбаума
слишком простая и предсказуемая, и потому ссылки на влияние точности
вычислений сразу за значением коэффициента С=3,57
выглядят как-то не очень убедительно. Это потребовало проверки.
Мы решили поэкспериментировать с формулой,
проверить излагаемые в статьях данные и смоделировать процесс отражения
результатов вычислений на экране монитора. Мы хотели увидеть хаос… и тот
предел порядка, за которым он начинается.
Что-то не вышло у нас
реализовать получение графика в специальных математических программах, и мы
решили сделать простенькую программу для получения результата на экране
компьютера. Ну, не сильны мы в тонкостях программирования, в языках, и
потому в качестве основы взяли старый добрый Паскаль. На нем мы хоть что-то
могли сделать. И сделали.
Первый результат еще больше озадачил. График получился, он походил на исходный
рис.1. Но, резкие черные полосы пустоты удивили. И хоть об этих полосах нам
было известно еще до начала наших исследований, вопрос остался. Как они
могли появиться в условиях случайной вероятности, т.е. в пространстве
«шумового хаоса»?
И еще, вот что пишет А.Пайс [5]:
«Внутри режима хаоса можно найти
бесконечное число всё уменьшающихся областей значений r,
для которых система вновь становится периодичной. Поведение этого логистического уравнения, которое, на первый взгляд,
выглядит таким элементарным, в высшей степени удивительно.»[5]
А.Пайс говорит о логистическом
уравнении:
|
xn+1 = f (xn ), где f (x) = rx(1 – x),
|
(3)
|
По этим словам математика А.Пайса хаос
может на коротком отрезке графика снова превращаться в порядок, а потом
назад … в хаос, … каким образом? Что-то уж совсем интересно становится…
Черно-белое поле графика
никаких ответов на поставленные вопросы не давало. Начальная кривая,
фрактальное дерево, белое поле хаоса с черными полосами – вот, почти и всё. Правда, при увеличении масштаба
изображения стало видно, что в черных «щелях» довольно четко
просматриваются … новые фрактальные образования. Они каким-то неведомым
образом очень четко, одной линией, вырастают из белого поля, ветвятся,
расширяются и … снова пропадают в новом отрезке белого поля хаоса. Больше ничего из этой картинки выжать не
удалось. Так это и есть хаос? Или
его надо искать где-то в другом месте? Какой-то странный хаос…
Нет, надо искать
действительный хаос. К этому подталкивало нас и интересное высказывание самого
Фейгенбаума:
«Мы
знаем, что детерминированные и простые закономерности могут вести
себя статистическим (или случайным) образом. Так, в современных компьютерах
имеются симулирующие хаотический процесс «генераторы случайных чисел».
Такие генераторы просто передвигают запятую в рациональном числе с
достаточно длинным периодом. Соответственно, можно предсказать, каким будет
n-е полученное число. И всё же последовательность полученных таким
образом чисел производит впечатление настолько неупорядоченной и случайной,
что все статистические тесты подтвердят случайное происхождение этих чисел.
Это явление обозначается термином «псевдослучайность».
Мы рассмотрим в данной работе, не являются ли псевдослучайными различные
хаотические природные процессы (вопреки сложившемуся, но ошибочному мнению,
что это не поддаётся проверке). То, что некоторые очень простые алгоритмы
для получения случайных чисел ведут себя полностью аналогично естественным
случайным процессам, представляется совершенно замечательным.» [1]
Конечно, мы предполагали, что
«хаос», получаемый по формуле Фейгенбаума, может быть и некая
«псевдослучайность». Но, все же, мы надеялись
получить визуальную картинку плавного перехода фрактальной структуры
графика в случайный «шумовой» фон хаоса. Примерно так: вот все учащающаяся
фрактальная структура, и, … всё, дальше равномерный шумовой фон случайных
значений. Но если этот «хаос» моделируется формулой, то … это тем более
надо увидеть
По сравнению с 70-ми годами
прошлого века, когда над этой формулой работал М.Фейгенбаум,
сегодня возможности компьютера несколько возросли, сейчас компьютер
позволяет вычислять числа с точностью более 25 знаков после запятой, и уже, кажется, можно разобраться, с
каким хаосом мы имеем дело в первом приближении.
Главным пунктом наших
исследований оказалось нахождение путей реализации вот этого высказывания Фейгенбаума:
«Поведение
шумового сигнала нерегулярно и трудно предсказуемо. Если, однако,
проанализировать достаточно длинную запись такого сигнала, может
обнаружиться, что его амплитуда находится в определённом узком диапазоне
определённую долю времени. Если анализ другой записи сигнала обнаружит
такую же долю времени, мы сможем описать шум статистически. Это
значит, что хотя и нельзя предсказать, какова будет следующая амплитуда, но
вполне возможно оценить вероятность достижения сигналом каких-то
определённых значений. За последние сто лет утвердился именно
статистический подход к неупорядоченным процессам.» [1]
Действительно, если
процесс получения результата, по
заявлениям ученых, выходит за рамки вычислительных возможностей компьютера,
то основным фактором обнаружения общей закономерности становится
статистический подход.
Полученный нами черно-белый
график изменения значения переменной Х в зависимости от коэффициента С способом итераций не внушал нам никакого уважения.
Да, мы получили примерно ту картинку, которую видели на рис1. и 2. Белое поле «хаоса» перечеркивалось четкими
пунктирными черными линиями
различной ширины. Пустота, она всегда завораживает и требует
понимания. В «хаосе» случайных значений, как и предсказывалось, есть четкий
порядок.
Тогда программа вычислений и
отображения их результатов была переделана. Был введен элемент изменения
цвета пиксела отображения при многократном совпадении
результата. Цвет пиксела меняется по 16-ти
цветной шкале стандартного монитора SVGA, принятого в Паскале. От
черного, через синий, красный, … и
так до белого при 16 кратном совпадении. Размер экрана 640 на 480 пикселов. Теперь мы можем задать циклы расчетов,
многократно превышающие количества отображаемых точек на мониторе. И
смотреть, как меняется статистическая вероятность совпадения результатов
вычислений в отдельных точках области экрана. Чем светлее точка, тем больше
в ней отражено совпадений результатов вычислений.
Статистический подход оценки
вычислений позволил резко изменить картинку.
Первый полученный результат на
рис.3.

Рис.3.
Статистический график для формулы Фейгенбаума.
Применение статистического подхода
к фиксации результатов вычислений
изменило вид графика. Он приобрел объемность. Вот теперь можно
переходить к исследованиям…
На рис. 4. выделена область,
ранее называемая «апериодическими изменениями переменной». Тот самый
«хаос»…
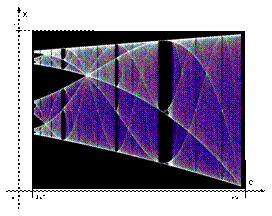
Рис.4.
Диапазон значений 3,57<С<4,0
Нам показалось, можно говорить
о чем угодно, но сложно отнести эту полученную картинку распределения
значений х в диапазоне изменения С от 3,57 до 4,0
к апериодическому распределению,
т.е. к «шумовому хаосу»…
Никакого случайного
распределения мы не увидели. Наоборот, четкое распределение значений, темные зоны с фрактальными
переходами, наложение зон изменения одной группы фракталов на другую с
созданием сложной картины…, порядок, который поддерживается даже при очень
большом увеличении разрешения, видимо, до предельной точности вычисления,
допускаемой компьютером.
На рис.5. мы ввели размерную
сетку для примерной оценки координат интересующих нас точек в области
статистических измерений 3,54<C<4,0 общего графика по формуле Фейгенбаума.
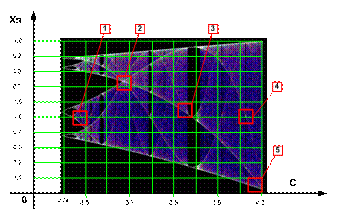
Рис.
5. График в координатой
сетке.
Конечно, в первую очередь,
обращает на себя внимание точка 2. Вот, на рис.6. ближайшие окрестности
этой точки.
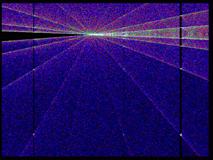
Рис.6. Окрестности точки 2.
На рис.7. снова показана точка
2 уже при большом увеличении масштаба. Как мы видим, четкость схождения
линий высокой статистической вероятности значений и при таком увеличении не
нарушается. Точности вычислений компьютера пока хватает для отражения
реальной картинки распределения. Её хватит и при увеличении масштаба еще на
порядок. Лишь затем появляются случайные элементы изображения.
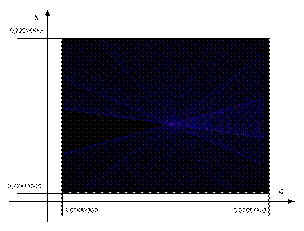
Рис.7. Точка 2. Пересечение линий высокой статистической
вероятности значений переменной.
Теперь посмотрим, как
рождается фрактальное образование. Это можно посмотреть на участке «щелей»,
темных вертикальных полос. На этих участках, как мы видим, значения
переменной концентрируются только в узких областях переходов, мостиков,
соединяющих края «щели». Таких участков в области отображения множество. Мы
намеренно взяли очень тонкую «щель», практически невидимую на общем
графике. Это точка 1 на рис.5. И, как видно на рис.8. картинка рождения
фрактала все же достаточно четкая.
Яркие белые области в темных
вертикалях на рисунке, это новые фракталы и новые «щели» меньшего размера.
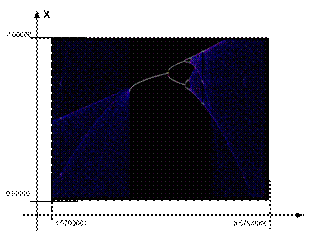
Рис.8.
Точка 1. Фрактальное образование в «щели».
Очень интересной
оказалось и точка 3 на рис.5. Вот область рождения фрактала, на рис.9.
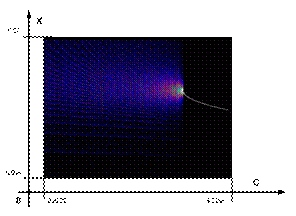
Рис.9.
Точка 3. Область сгущения линий высокой вероятности.
Полученная картинка
распределения статистической вероятности очень напоминает картину
оптической интерференции. Как нам представляется, это результат наложения
нескольких фрактальных сетей, образованных ранее при меньших значениях С. К
подобной области мы еще вернемся…
Несомненный интерес
представляет точка 5 на рис.5. Это граничная область графика.
Мы изначально выбрали значение
переменной х=0,5 для получений ограничения области значений Хn
при итерационных вычислениях. Действительно, при С
= 4 и Х1=0,5 по формуле Фейгенбаума Хn =0. Как оказалось,
это ограничение области отображения результатов вычислений действует и при
других начальных значениях Х.
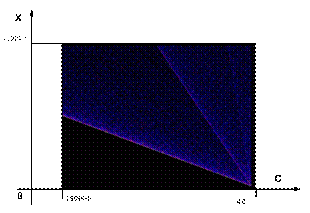
Рис.10. Точка5. Граничная область графика
распределения значений переменной по формуле Фейгенбаума.
Расчетная картинка на рис.10.
получена при Х1=0,4. Как это видно,
граница области определения никуда не сдвинулась. Аналогичная картина
наблюдается при любом начальном значении х в диапазоне от 0 до 1.
Ну, и наконец, точка 4
рисунка5. Как мы видим на рис.11. , картина вполне предсказуемая. В
«щели» образуется новая фрактальная
сеть. С одной стороны видимая концентрация линий высокой статистической
вероятности, а с другой – начало роста фрактального распределения…
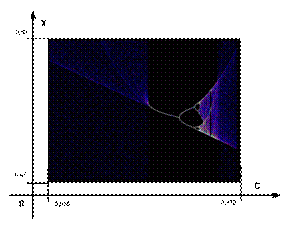
Рис.11.
Точка 4. Образование фрактальной сети.
Видимо, образование «щелей» в
наслоениях фрактальных ветвей и образование в них новых фрактальных
образований меньшего размера является общей закономерностью, определяемой
начальной формулой и результатом наложения.
Общее увеличение масштаба в
подборке фрагментов графика на рис.12. от первого до последнего более чем в
100 раз. Но и при таком разрешении хаос что-то не виден….
Видимо, это, так называемый
«странный» аттрактор. Зона резкого увеличения
статистической вероятности получения результата вычисления. В эту
зону стягиваются точки многих последовательностей Xn, вычисляемых от
разных значений Х1 .
Мы лишь увидели эту зону, но
как всё происходит, пока остается только догадываться…
  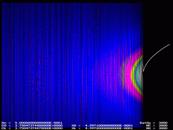 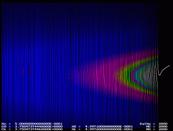 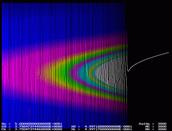 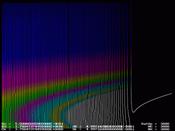
Рис.12.
«Странный» аттрактор – зона рождения фрактала
Последний фрагмент, по всей
видимости, это уже почти предел точности вычисления программы на Паскале,
но не компьютера. До сильного влияния погрешности вычисления компьютера на
результат мы еще, похоже, так и не добрались.
На последних фрагментах
рис.12. DatX-
количество выводимых на экран результатов вычислений цикла NX- количества вычислений
Хn
по вертикали. NC – количество
вычислений по горизонтали на взятом диапазоне изменения С. А также первое
заданное значение Xn, начальные значения X0 и С0, и конечные значения интервала изменения –
Xk и Ck,
соответственно. Эти данные и выведены на экран.
Четкая картинка достигается
при необходимой плотности вычислений. В общем случае, чем меньше объект
выбран для анализа из общего графика, тем большая плотность вычислений
необходима для получения достоверной картины. Но это не всегда соблюдается.
Иногда уже и начальная концентрация точек результатов на выбранном участке
графика так велика, что нет смысла в увеличении плотности вычислений при
скользящем масштабировании.
Применение метода графического
определения статистической вероятности получения результата в каждой точке
выделенного координатного пространства графика логистического
уравнения позволило выявить общую картину взаимовлияния фрактальных
образований, генерируемых изменением переменной Х и коэффициентом С в данном уравнении.
Как нам кажется, стало
понятно, что хаотического изменения итерационного результата вычислений во
всем интервале изменения С пока не наблюдается. И, например, уже можно дать некоторые
определенные ответы вот на это, как нам показалось, уже достаточно спорное
высказывание:
«В эксперименте не удается наблюдать бесконечную
последовательность бифуркаций удвоения, поскольку проявляется влияние
внешнего шума. Воздействием шума на динамику отображения занимался целый
ряд ученых, однако, эта проблема в общем виде не решена. Известно, что
дерево Фейгенбаума видоизменяется под действием
шума, причем его рассмотрение в разных масштабах демонстрирует свойства
универсальности».[9]
Как мы видим на графике
рис.5., бесконечную
последовательность бифуркаций удвоения по логистическому
уравнению получить, видимо пока
невозможно не из-за влияния внешнего шума, а по причине наложения одной
части фрактального образования на другую уже в начале его появления. Пока
проследить бифуркации можно только … до первой «звезды», точки пересечения
ветвей фрактала. Далее о предсказуемых точках бифуркации говорить уже,
действительно, трудно. Для этого надо еще и отслеживать наложение множества
фрактальных ветвей, которые на этом уровне исследований только
подразумеваются…
Как нам кажется, пока дерево Фейгенбаума демонстрирует свойство универсальности
только на фоне псевдохаоса, определяемого
начальными условиями формулы последовательности. Действительный «шум»
начинает действовать на много порядков ниже
и общей статистической картинки, кажется, почти не меняет.
Эксперименты этого этапа
закончены.
Хаоса от погрешности
вычислений по формуле Фейгенбаума на пределе
возможностей компьютера мы так толком и не увидели. Так, отдельные
фрагменты…
Хорошо это или плохо, … не знаем…
Екатеринбург
Сентябрь 2008г.
Литература:
1.
М. Фейгенбаум
Универсальность в поведении нелинейных систем. (Feigenbaum M. J. Universal Behavior in
Nonlinear Systems. — Los Alamos
Science. 1980, v. 1,
No. 1, pp. 4–27.)
Перевод С. Г. Тиходеева.
http://ega-math.narod.ru/Nquant/Feigen.htm#note
2.
Антон
Никифоров Метод расчета скейлинговых
констант Фейгенбаума для одномерных дискретных
отображений по точкам сверхустойчивых циклов.
3.
Введение в фракталы
Информатика .http.//inf.1september.ru/2000/6/fract/
4.
О фракталах и
их алгоритмах. http://fract.narod.ru/about.htm
5. А. Пайс. Гении науки
(Перевод с английского Е. И. Фукаловой.
Под редакцией к.ф.-м.н.
С. Г. Новокшенова). — М.: Институт компьютерных
исследований, 2002, 448 с. ISBN 5-93972-168-0 (Abraham
Pais. The Genius of Science (A
Portrait Gallery). Oxford
University Press,
2000). http://ega-math.narod.ru/Reid/Pais.htm
6.
ЛОГИСТИЧЕСКОЕ
ОТОБРАЖЕНИЕ. http://www.math.rsu.ru/mexmat/kvm/MME/dsarch/logist.html
7.
С.В.Поршнев Моделирование хаотического поведения
динамических систем.
http://www.nsu.ru/matlab/Exponenta_RU/educat/systemat/porshnev/chaos/chaos.asp.htm
8.
Моделирование
развития леса. http://www.keldysh.ru/pages/forest/forest/25.htm
9.
Сложная динамика схемы на переключаемых
конденсаторах: Учебно-методическое пособие.
http://window.edu.ru/window_catalog/pdf2txt?p_id=13195&p_page=2
|