|
Мы ищем
хаос… - 2.
Мы продолжаем публикацию результатов
исследования разностного логистического
уравнения, затронутого в нашей статье [10].
Хотелось бы сразу отметить, что графики, показанные, как результат
вычислений по заданной формуле последовательности несколько приукрашены.
Они лишены первичных колебаний значений, неизбежных при подходе к режиму
стабилизации.
Но, это было сделано с той же целью, с которой то же самое делали и остальные
авторы публикаций – необходимо было отразить основной процесс фрактализации результатов вычислений, не зарываясь в
частности подхода к этому. Пока, не зарываясь…, показать основу, главный
результат – фрактал.
У нас была и дополнительная
цель – выяснить влияние «шума», ошибки вычисления на пределе возможности компьютера,
апериодической составляющей на результирующий график. До существенного
влияния «шума» на результат мы так и не добрались. Широкий
скейлинг (скользящее масштабирование) по
различным областям графика на уровне точности программы сильного влияния не
выявил. Обещанного хаоса за С=3,57 мы так и не увидели…
А.Пайс [5] призрачно намекает, что при изменении
начального значения х основной график логистического уравнения претерпевает незначительные изменения.
Какие?
Если использовать методику
отражения только стабилизированных значений вычислений, как это и делали
авторы многих публикаций, то … при любом начальном х график стоит как вкопанный,
никаких особых изменений незаметно. Но, тогда, какой смысл смотреть на эту
застывшую картину бесконечной фрактализации…?
Изменения проявляются, если каждый раз, при взятии нового значения х1 отражать все точки вычислений. Вот тогда
видны изменения в подходе к зонам стабилизации результата.
 
Рис.1
Графики при х=0,1 (слева) и х=0,5
( справа)
Для примера на рис.1. покажем,
как меняется вид графика при изменении начального значения х . Взяты значения х=0,1,
как один из вариантов подхода к оптимальному значению и оптимальное
значение х=0,5, при котором
квадратичная функция х(1-х) достигает максимума. При х=0,5, как мы видим, количество
точек за пределами основного графика минимально.
При переходе через максимум
при х=0,5 отмечается
симметричность картины. Вот, на рис.2. показаны сформированные графики при х=0,4 и х=0,6. Что называется, найдите разницу…
 
Рис.2.
Графики при х=0,4(слева) и х=0,6 (справа)
Более интересен подход начального значения переменной х к границе диапазона
изменения. На рис. 3. показаны графики сверху вниз при х=0,1; х=0,01; х=0,00001 и х= 0,00000001 соответственно.




Рис.3.
Графики при х=0,1; х=0,01; х=0,00001; х=0,00000001
(сверху
вниз)
Как мы видим, при всех
изменениях начального значения х основной график
существенных изменений не претерпевает. Меняются лишь подходы к точкам
стабилизации, которые и составляют основной график. При подходе к границе
х=1 картина будет аналогичная.
По мере приближения к границе
диапазона возникают новые точки стабилизации, например, при х=0,00000001, как мы видим, возникли
уже две относительно стабильные точки, соединяющие в единую линию точку пересечения
фрактальных образований («звезду») с начальной линией роста до входа в фрактальную область. Эта линия и дальше хорошо прослеживается на основном графике
при соответствующем изменении масштаба отображения…
Да, запланированного, вроде бы, хаоса или
апериодического изменения очередного вычисленного хn в процессе подхода к точке стабилизации и
здесь что-то не видно…
Механизм образования фракталов
при вычислениях значений хn по формуле разностного логистического уравнения хорошо изложен в работах Митчелла Фейгенбаума [1], основного исследователя этого и других
уравнений подобного типа, и потому
возвращаться к этому мы не будем.
По всей видимости, разностное логистическое уравнение вида:
является основным уравнением
для уравнений вида:
где k может
принимать любое положительное значение. Это верхняя граница изменения
переменной х.
При этом начальная точка
образования общего графика r1 при х=0,
может быть вычислена как r1=1/k, а конечная точка, соответственно, как rк=4/k, при достижении которой значения хn
выходят за пределы диапазона изменения х.
Для примера можно взять k=Ф, где Ф = 1,618…, золотая пропорция или число Фидия.
Уравнение принимает вид:
Где: 0<xn<1,618…
Точка начала графика r1=1/Ф = 0,618…, конечная точка графика rк =4/Ф = 2,4721359…
Построение графика при х1=0,618…
на рис.4. подтверждает полученные результаты предварительных расчетов
диапазона изменения r.
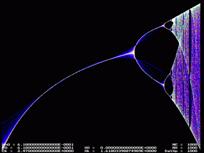
Рис.4.
График, построенный по формуле (3).
Как мы видим, форма графика
при расчетном масштабировании никаких заметных изменений не претерпевает.
Изменения графика появляются
при преобразовании формулы (2) до
вида:
Например, модифицируем
формулу(3) до вида:
На рис.5. показан график,
построенный по формуле (5). Как мы видим, график значительно изменился.
Появились новые фракталообразующие щели. Изменился
ход линий высокой вероятности. Начальная точка графика сместилась к r1=0,38, конечная точка rn=3,43. Изменился и диапазон изменения
переменной х от 0 до значения 2,23.
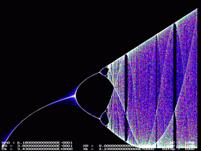
Рис.5.
График, построенный по формуле (5).
Изменим уравнение до вида:
Увеличение степени приводит к
новому изменении графика. Например, на рис.6. видно, что при диапазоне изменения х от 0 до Ф,
начало графика сместилось до r1= 0,236,
а конечная точка сместилась к rn=2,236..
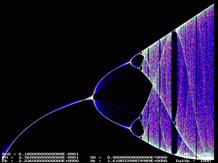
Рис.6.
График, построенный по формуле (6).
Теперь модифицируем уравнение
до вида:
При этом график уравнения
изменился. На рис.7. слева график по
формуле (7) при m=2, справа при m=3, соответственно.
Начальное значение х1 =0,9 в обоих случаях.
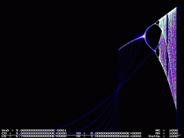 
Рис.7.
Графики по формуле (7) при m=2
(слева), m =3
(справа).
При увеличении степени m происходит увеличение области отображения, но общая
картина меняется незначительно.
На этом эксперименты с
модификациями уравнений, сконструированными на основе разностного логистического уравнения можно бы и закончить, но … нас
несколько озадачил исторически ограниченный аспект проведенных ранее
исследований.
Изначально, уравнение (1) было
предложено, как формула расчета колебаний средней численности какой-то
популяции какого-то биологического вида, в замкнутом объеме за несколько
периодов, в зависимости от благоприятности условий размножения r (или С).
Далее вводятся необходимые
ограничения. При r<1
численность популяции стремится к 0, т.е. к вымиранию, стабильное развитие
возможно только при r>1. При увеличении r до какого-то значения
рост популяции идет стабильно, но, далее вдруг возникают колебания
численности. При дальнейшем росте коэффициента r непрерывная линия графика рвется. Сначала возникают
две точки стабилизации, потом четыре, и т.д. Удвоение точек бифуркации
продолжается недолго, и уже после
нарастания таких точек до какого-то из 2n значений
за одно очередное колебание общей линии графика переходит в апериодический
характер изменений. Количество точек
бифуркации на предполагаемой линии графика принимается за количество
периодов изменения численности, а весь период очередного колебания этой
линии графика интерпретируется как период измерения при заданном изменении r. Понятно, что всё построение зависит от взятого шага
изменения r в
исследуемом диапазоне изменения. Чем меньше шаг, тем плавнее
начальный изгиб общей линии колебаний. Но, уравнение квадратное, и
колебания все время ускоряются, переходя в апериодическое изменение. Да и привычной линии графика нет, одни
точки, которые можно привязать к любой умозрительно взятой линии.
Это и заставило построить
общий график, примерно такой, как на рис.1.
Теперь стало возможным решать
обратную задачу, определять изменения r для получения
заданного колебания переменной х. Уравнение стало логистическим…
Область применения уравнения
для решения практических задач резко расширилась. Но, историческое
ограничение области изменения фактора r от 0 до 4 так и
осталось.
Если ограничение увеличения r до 4 математически обоснованы, то изменение r в область отрицательных значений
ничем другим, кроме исторически сложившегося представления о применении
уравнения, не ограничены.
Для такого расширения
диапазона изменения r необходимо ввести и
отрицательные значения хn . Пока при положительном
начальном х1.
Результат на рис.8.

Рис.8.
Полный график логистического разностного
уравнения.
График получен при начальном
значении х1=0,5.
Диапазон изменения r от -2
до 4, диапазон изменения хn от -1 до
1,6. За границами этого диапазона r построение графика
срывается. При отрицательном
начальном значении х1 построение графика у нас не получилось…
Как мы видим, график содержит
две группы фрактальных образований, одна нам уже известна, вторая
располагается в отрицательной области значений r и
захватывает диапазон изменения хn от -1
до 1,5. Видимо, эта область требует отдельного исследования, специалистами,
к коим мы себя причислить не можем…
А вот, на рис.9. результат
построения графика по экзотической, смоделированной нами формуле:
|
хn+1= xn Logфr (ф-хn)
|
(8)
|
Где Logфr = Ln r/Lnф ;

Рис.9.
График, построенный по формуле (8).
Как мы видим, общая форма графика
остается стабильной. Это, видимо говорит об общем характере графической картины результатов вычислений этого класса уравнений.
Программа написана
на языке Турбо Паскаль версии Borland Pascal with Objects 7.0 выпуска еще
90-х годов прошлого века…
Приводим полный листинг программы:
{Программа
Графический
вывод результатов расчета логистического
уравнения Xn+1 = Cn*Xn*(1-Xn)}
Uses Crt,
Graph;
Const Esc = #27;
Var Gd,
Gm, C, X, Cs, Xs, Cp, Xp, NC, NX, DatXp,
i, j, n, d: Integer;
C0, Ck, X0, Xk, mC,
mX, dC, dX, Xn, Xn0, Cn: Double;
Color, Xt: integer;
s, s1, s2, G: string;
f: file of char;
ch, ch1, ch2, ch3, Ch4: char;
n1, n2, n3: char;
bmp: array [1..40] of char;
function OutNumIn (L: Integer) : string; {подпрограмма вывода целых чисел}
var
S: string;
begin
Str
(L, S);
OutNumIn:=
S;
End;
function OutNumRe (L: Double) : string; {подпрограмма вывода вещественных чисел}
var
S: string;
begin
Str
(L, S);
OutNumRe:=
S;
End;
label start;
Begin
Randomize;
n:= 1; {Начальные значения программы при
первом запуске: }
Xn0:= -0.5;
C0:= -2; { Начальное
значение коэффициента С, задаваемое для расчета }
Ck:=
4; { Конечное
значение коэффициента С, задаваемое для расчета }
X0:= -1.6; { Начальное
значение Х, задаваемое для графика }
Xk:=
1.5; { Конечное
значение Х, задаваемое для графика }
NC:= 1000; {Число задаваемых значений С для
расчета }
NX:= 1000; { Число
вычисляемых значений X - итерации}
DatXp:=
1000; { Число
выводимых на экран значений X до
конечного NX }
Ch:= #0;
Cs:= 620; { размер
экрана по горизонтали }
Xs:= 460; { размер
экрана по вертикали }
n1:= #0;
n2:= #227;
n3:= #255;
bmp[1]:=
#66; bmp[2]:= #77;
bmp[3]:= #54; bmp[4]:=
#16;
bmp[5]:= #14; bmp[6]:= #0;
bmp[7]:= #0; bmp[8]:=
#0;
bmp[9]:= #0;
bmp[10]:= #0; bmp[11]:=
#54; bmp[12]:= #0;
bmp[13]:= #0; bmp[14]:= #0; bmp[15]:= #40; bmp[16]:= #0;
bmp[17]:= #0; bmp[18]:= #0; bmp[19]:= #128; bmp[20]:= #2;
bmp[21]:= #0; bmp[22]:= #0; bmp[23]:= #224; bmp[24]:= #1;
bmp[25]:= #0; bmp[26]:= #0; bmp[27]:= #1; bmp[28]:= #0;
bmp[29]:= #24; bmp[30]:=
#0; bmp[31]:= #0; bmp[32]:= #0;
bmp[33]:= #0; bmp[34]:= #0; bmp[35]:= #0; bmp[36]:= #16;
bmp[37]:= #14; bmp[38]:=
#0; bmp[39]:= #0; bmp[40]:= #0;
start:
Gd:=Detect;
InitGraph(Gd, Gm, ''); { открытие графического режима }
If GraphResult
<> grOk Then Halt(1);
dC:= Ck-C0;
mC:= dC/NC; { масштаб для вывода С
}
dX:=
Xk-X0;
mX:= dX/NX; { масштаб для вывода X
}
for C:= 0 to NC do { цикл изменяемых значений для С }
begin
Cn:=
C0+C*mC;
Xn:= Xn0;
For X:= 0 to NX do { цикл
изменяемых значений для Х }
begin
Вот
здесь надо сделать остановку. Это основная вычислительная часть программы:
Xn:= Cn*{(1-(1-Random(2))/50)*}Xn*(1-Xn); { вычисление
Xn+1 }
Уравнение
корректиректируется в зависимости от поставленных задач. Сейчас это логистическое уравнение с элементом случайного
распределения ( он временно выключен из
уравнения).
If X > (NX-DatXp) then
begin
Cp:=Round((Cn-C0)/dC*Cs+10); {координата пиксела
по горизонтали }
If (Xn
>= X0) and (Xn <= Xk)
then
Xp:=Round(Xs*(1-(Xn-X0)/dX) + 10) Else Xp:=500; { координата пиксела по вертикали }
Color:=GetPixel(Cp, Xp); { проверка
предыдущего пиксела с экрана}
If Color > 0 Then
Color:=Color+1
else Color:=1;
If Color > 15
then
Color:=15;
PutPixel (Cp, Xp,
Color); { запись пиксела на экран }
end;
end;
end;
S:=
' Press any key - to continy, or Esc - to quit. Please,
white 20..40 seconds';
OutTextXY
(1, 1, S); { вывод
текста на экран в графическом режиме }
S:= 'Xn0 =';
OutTextXY
(10, 450, S);
S:= OutNumRe(Xn0);
OutTextXY
(50, 450, S);
S:= 'C0 =';
OutTextXY
(10, 460, S);
S:= OutNumRe(C0);
OutTextXY
(50, 460, S);
S:= 'Ck =';
OutTextXY
(10, 470, S);
S:= OutNumRe(Ck);
OutTextXY
(50, 470, S);
S:= ' X0 =';
OutTextXY
(260, 460, S);
S:= OutNumRe(X0);
OutTextXY
(310, 460, S);
S:= ' Xk =';
OutTextXY
(260, 470, S);
S:= OutNumRe(Xk);
OutTextXY
(310, 470, S);
S:= ' NC =';
OutTextXY
(520, 450, S);
S:= OutNumIn(NC);
OutTextXY
(590, 450, S);
S:= ' NX =';
OutTextXY
(520, 460, S);
S:= OutNumIn(NX);
OutTextXY
(590, 460, S);
S:= 'DatXp =';
OutTextXY
(520, 470, S);
S:= OutNumIn(DatXp);
OutTextXY (590,
470, S);
If n>1 then { условие записи графики при повторных проходах
программы}
begin
assign
(f,s2); { открытие графического файла }
rewrite (f);
for i:= 1 to 40 do { запись
установочных кодов формата графического файла }
Write (f, bmp[i]);
Write (f, ch);
Write (f, ch);
For j:= 479 downto 10 do { цикл записи ?строка за строкой? }
begin
For i:= 0 to 639 do { цикл записи ?пиксел за пикселом? }
begin
Color:= GetPixel (i,j); { запись пиксела в файл }
If Color=0 then
begin ch1:= n1;
ch2:= n1; ch3:=n1; end; { замена цвета пиксела из файла *.pas в формат файла *.bmp }
If Color=1 then
begin ch1:= n2;
ch2:= n1; ch3:=n1; end;
If Color=2 then
begin ch1:= n3;
ch2:= n1; ch3:=n1; end;
If Color=3 then
begin ch1:= n2;
ch2:= n1; ch3:=n2; end;
If Color=4 then
begin ch1:= n2;
ch2:= n1; ch3:=n3; end;
If Color=5 then
begin ch1:= n1;
ch2:= n2; ch3:=n2; end;
If Color=6 then
begin ch1:= n1;
ch2:= n3; ch3:=n1; end;
If Color=7 then
begin ch1:= n3;
ch2:= n1; ch3:=n3; end;
If Color=8 then
begin ch1:= n3;
ch2:= n2; ch3:=n1; end;
If Color=9 then
begin ch1:= n2;
ch2:= n3; ch3:=n1; end;
If Color=10 then
begin ch1:= n1;
ch2:= n2; ch3:=n3; end;
If Color=11 then
begin ch1:= n3;
ch2:= n2; ch3:=n1; end;
If Color=12 then
begin ch1:= n2;
ch2:= n3; ch3:=n3; end;
If Color=13 then
begin ch1:= n3;
ch2:= n3; ch3:=n2; end;
If Color=14 then
begin ch1:= n3; ch2:= n2; ch3:=n3; end;
If Color=15 then
begin ch1:= n3;
ch2:= n3; ch3:=n3; end;
Write (f,
ch1);
Write (f, ch2);
Write (f, ch3);
end;
end;
For j:= 9 downto 0 do
begin
For i:= 0 to 639 do
begin
Write (f, ch);
Write (f, ch);
Write (f, ch);
end;
end;
For n:= 1 to 12 do
Write (f, ch);
Close(f); { закрытие
графического файла }
end;
inc(n);
Repeat
Until KeyPressed;
CloseGraph; { закрытие графического
режима }
Ch4:= ReadKey;
If Ch4 = #0 then Ch4:= ReadKey;
If Ch4 <> Esc then
begin
Write ('0
<Xn0< 1 = ',Xn0,' ');{вывод
значений на экран в текстовом режиме и ввод новых значений}
Readln (Xn0);
Writeln;
Write ('0 <C0< 4 =
',C0,' ');
Readln
(C0);
Write ('0 <Ck< 4 =
',Ck,' ');
Readln
(Ck);
Writeln;
Write ('0 <X0< 1 =
',X0,' ');
Readln
(X0);
Write ('0 <Xk< 1 = ',Xk,' ');
Readln
(Xk);
Writeln;
Write ('100 <NC<
20000 = ',NC,' ');
Readln
(NC);
Write ('100 <NX<
20000 = ',NX,' ');
Readln
(NX);
Write ('0 <DatXp< NX
= ',DatXp,' ');
Readln
(DatXp);
Writeln;
Write ('Enter filename (
*.bmp): ',s2,' '); { вывод имени графического файла на экран и ввод нового имени }
Readln (s2); { }
Goto start { возврат на повторение программы }
end;
end.
Можно только повторить, мы не
специалисты в программировании, и потому сначала решали только основную
задачу – вычисление с выводом результата на экран в графическом режиме. Мы
отказались от вывода в файл всех результатов вычислений, так как программа
нацелена на эксперимент, оперативный поиск интересных областей и их границ в пространстве графика, и
потому данные вычислений нас пока не очень интересовали. Тем более, что такой вывод делается очень быстро на любом этапе
исследований.
Остальные
блоки программы разрабатывались по мере необходимости в силу наших знаний и
умения. Конечно, программа нуждается в большой доработке и оптимизации.
Специалисты только усмехнутся, глядя на такой уровень программирования, но
… уж, извините, решали задачу, как умели.
Да, приходится констатировать,
что на всех этапах проведенного исследования никакого особого влияния
погрешность компьютерного вычисления на общую картину получаемого графика
не оказывает. Обещанного хаоса мы так и не обнаружили. Скейлинг
(скользящее масштабирование) на отдельных участках графика также пока не
выявил серьезного влияния «шумовой» составляющей на общую картину.
Пришлось ввести «хаос»
искусственно. На рис.10. результат введения
случайной вероятности по формуле:
|
Xn:= Cn*(1-(2-Random(2))/4)*Xn*(1-Xn);
|
(9)
|
Полученная картинка разительно
отличается от всех ранее построенных графиков. Теперь это только линии
высокой вероятности с четкими точками
пересечений, а не расплывчатыми зонами, как могло бы представляться. Фракталов нет. Только плавные изгибы
множества линий. Такой
запланированный «хаос» влияет вполне
определенно.

Рис.10.
Введение случайности в результат
вычислений по формуле (9).
Понятно, «псевдохаос»,
он предсказуем…, хотя бы отчасти.
На этом мы закончили наши исследования логистического
уравнения с вариациями на вольную тему.
Их результаты перед Вами.
Как нам представляется, это только малый шаг на пути к пониманию. Возможно,
эти материалы помогут специалистам в настоящих исследованиях логистического уравнения.
Последнее слово еще не
сказано…
г. Екатеринбург
Сентябрь 2008г.
Литература:
1.
М. Фейгенбаум
Универсальность в поведении нелинейных систем. (Feigenbaum M. J. Universal Behavior in
Nonlinear Systems. — Los Alamos
Science. 1980, v. 1,
No. 1, pp. 4–27.)
Перевод С. Г. Тиходеева.
http://ega-math.narod.ru/Nquant/Feigen.htm#note
2.
Антон
Никифоров Метод расчета скейлинговых
констант Фейгенбаума для одномерных дискретных
отображений по точкам сверхустойчивых циклов.
3.
Введение в фракталы
Информатика .http.//inf.1september.ru/2000/6/fract/
4.
О фракталах и
их алгоритмах. http://fract.narod.ru/about.htm
5. А. Пайс. Гении науки
(Перевод с английского Е. И. Фукаловой.
Под редакцией к.ф.-м.н.
С. Г. Новокшенова). — М.: Институт
компьютерных исследований, 2002, 448 с. ISBN 5-93972-168-0 (Abraham Pais. The Genius of
Science (A Portrait Gallery). Oxford
University Press, 2000).
http://ega-math.narod.ru/Reid/Pais.htm
6.
ЛОГИСТИЧЕСКОЕ
ОТОБРАЖЕНИЕ. http://www.math.rsu.ru/mexmat/kvm/MME/dsarch/logist.html
7.
С.В.Поршнев Моделирование хаотического поведения
динамических систем.
http://www.nsu.ru/matlab/Exponenta_RU/educat/systemat/porshnev/chaos/chaos.asp.htm
8.
Моделирование
развития леса. http://www.keldysh.ru/pages/forest/forest/25.htm
9.
Сложная динамика схемы на переключаемых
конденсаторах: Учебно-методическое пособие. http://window.edu.ru/window_catalog/pdf2txt?p_id=13195&p_page=2
10. А.В.Никитин, В.Ю.Ипатов. Мы ищем хаос…
|