Число.

Давайте-ка, поподробнее разберемся с числом. Что есть – число?

Сегодня понятие числа включает в себя наполнение числа и его изображение. Об этом уже сложно говорить, настолько эти понятия привычны. И всё же …

Человек считает давно. Начиналось все, наверное, с камешков, палочек. Чтобы как-то запомнить полученное количество, надо как-то это изобразить… и назвать. Собственно, количество и стало основным критерием в понятии числа. Для нас число и обозначает количество чего-либо…. Результат счета. Вернее, форма запоминания этого количества. А привычное 1,2,3,… — первый счетный процесс. Любое число можно представить суммой единиц. N=1+1+1+1+…

Сколько палочек в коробке? Начнем вынимать по одной и считать. Можно наоборот, складывать палочки в коробку. В любом случае на последней палочке счет кончается. Это и будет количеством палочек в коробке или результат счета. Можно все единицы выставить в одну длинную цепочку, а можно сложить кучками — кому как удобнее. А как удобнее? И для чего…?

Изображение числа неразрывно связано с применяемой системой счисления. И требует организации. Постепенно были придуманы цифры и разработаны формы записи числа. Они и образовали различные системы. Сегодня изображение числа и определяется этими понятиями.

Итак, число – результат счета. В какую бы систему мы не вкладывали этот результат, количество единиц от этого не изменится. Меняется только форма записи. Числа получаются разные, а смысл их один и тот же — количество единиц.

Основная применяемая сегодня форма записи числа – позиционная. Т.е. число состоит из разрядов и в каждом разряде цифра. А разряд – новая степень основания счетной системы. Такая запись числа и определила название систем счисления. Позиционные. Каждый разряд имеет свое место в составе числа.

Форма записи числа и система счисления определяет применение и решаемые задачи. И наоборот, конкретная задача определяет применение той или иной системы счисления. Это две стороны одной медали. Очевидно, это определяется требованиями, которые мы предъявляем к форме записи числа и возможностями проведения дальнейших действий. Вот как определяет число Ньютон: «Под числом мы понимаем не столько множество единиц, сколько отвлеченное отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу».

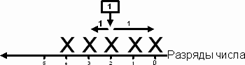
Рис. 14. Число на разрядной оси.

Видимо, это основное определение числа. Число — это количество или отношение….

Алгебра дает расширение понятия числа и вводит его кодирование. Под числом А, например, понимается какое-либо число из известных нам. Под числом Х, У, неизвестные, которые надо найти решением. Алгебра же ввела понятие постоянной и переменной величины для числа.

Число стало и величиной, переменной, постоянной, кодированной, известной и неизвестной, но все так же — это количество и отношение….

На рис.8. показано число, установленное на разрядной оси, в соответствии с позиционным представлением, неизвестной системы счисления, неизвестной разрядности и наполнения разрядов. Какое-то число, какой-то системы счисления установлено на разрядную ось….

Под неизвестными Х скрываются разряды числа установленного на разрядную ось. Фактически, одну неизвестную Х мы заменили ее разрядным эквивалентом на разрядной оси. Теперь, по мере роста числа разрядные неизвестные фиксируют заполнение очередного разряда числа, не определяя его. Каждому разряду можно было бы дать свою неизвестную, но это нецелесообразно, т.к. таким изображением мы определяем только изменение разрядного состава числа. С ростом числа растет и количество используемых разрядов на разрядной оси.

Число стало цепью переменной длины из связанных разрядов неопределенного наполнения.

Будет ли такое изображение числа соответствовать его определению?

Очевидно, будет. Только надо многое уточнить, чтобы это число стало определенным и конкретным. Но, такое изображение числа может раскрыть некоторые его свойства, ранее невидимые.

Представленный вариант изображения числа позволяет отказаться от его конкретного количественного наполнения, но оставить позиционную форму представления и изображения.

Разряды числа

Число состоит из разрядов. В разрядах, как в корзинках, находятся единицы соответствующего «веса». Количество единиц в разряде может быть любым, но не больше «вместимости» этой корзины — разряда. Если разряд уже «полный», то попадание в него очередной единицы вызывает его «переполнение» и «обнуление», т.е. перебрасывания всего содержимого в следующий разряд, как очередной единицы счета, теперь уже «веса» этого разряда. Понятно и привычно. Но если отбросить понятие «вес», такой процесс представляется как движение единицы по разрядам числа. Такое движение возможно только при определенных условиях, в частности при переполнении разряда. Процесс переполнения и обнуления разрядов может начаться только с разряда сложения и продолжаться до незаполненного разряда. Под разрядом сложения мы понимаем тот разряд числа, в котором производится операция сложения.

Уточним понятия заполнение и переполнение разряда.

Пустой разряд – отсутствие единиц в разряде.

Неполный разряд – в разряде имеются единицы, но их количество, более чем на одну единицу меньше основания счетной системы.

Разряд можно считать полным, если количество единиц в разряде на единицу или ее долю меньше основания счетной системы.

Разряд можно считать заполненным, если в нем находится количество единиц, равное основанию системы. Это состояние кратковременное и заполнение разряда предполагает последующую операцию — обнуление. При этом из всего содержимого разряда формируется единица следующего и передвигается туда, а этот разряд остается пустым.

Переполнение разряда возникает, если в нем находится количество единиц больше, чем основание системы счисления. Понятно, что это такое же кратковременное состояние, как и заполнение разряда. Далее формируется единица с весом следующего разряда числа, а остаток или остается в этом разряде, если есть целые единицы этого разряда, или он распределяется в младших разрядах по весу единиц остатка. Как, например, в системах счета с иррациональным основанием.

Видимо, к разрядным математическим операциям следует отнести только две — сложение и вычитание. Остальные математические действия производятся над числами, а на разрядах лишь отражаются. Как результат вычислений. Или как методика и программа действий по программе изменения числа. Умножение, деление, возведение в степень и т.д. – действия над числами.

Числовая цепь.

Цифровая запись применима для нескольких конструкций. Самая распространенная – число в позиционной форме. Каждая цифра – разряд.

Следующая форма цифровой записи – цифровая последовательность. Такая последовательность не имеет разрядов, и не может называться числом, просто последовательное расположение цифр. Например, номер телефона. Она может быть ограничена в количестве мест, а может и не иметь ограничений по длине. Цифровая последовательность фиксированной длины часто называется словом, машинным словом, байтом и т.д. Термин меняется в зависимости от длины цифровой последовательности. Иногда, под эти обозначения попадают и числа фиксированной длины или разрядности. Но это уже издержки терминологии.

В общем случае, длина числа ничем не ограничена. И если нам всё равно, какой вес имеют единица самого старшего разряда этого числа, тем более, что мы намеренно рассматриваем число в режиме постоянного роста, то имеет прямой смысл рассматривать только ограниченную часть неограниченно растущего числа. Например, только первые десять разрядов. Все остальные разряды числа, хоть и имеются, но нас они уже не интересуют. Нас интересует только эта часть числа, ограниченная первыми десятью разрядами. Если, вместо чисел мы рассматриваем их отдельные части, которые единого числа уже не представляют, но состоят из последовательности цифр, составляющих часть какого-то бесконечно большого числа, то эту часть числа и можно назвать числовой цепью. Числовая цепь может иметь ограничения. Смысл ограничения заключается в ограничении влияния единицы переполнения движущейся по числовой цепи в процессе преобразования числа. Введем ограничение контроля. Ну, например – С – «стоп контроля». Всё, что далее, нас не интересует и не влияет на этот ограниченный участок.

Если единица переполнения при движении влево, за пределы установленного нами контрольного разряда, перестает влиять на числовую цепь, и не изменяет ее состояния, то мы говорим, что числовая цепь ограничена слева или сверху и записываем ее как С1010101010 ….

Если единица переполнения при движении вправо, за пределы установленного нами контрольного разряда, перестает влиять на числовую цепь, и не изменяет ее состояния, мы говорим, что числовая цепь ограничена справа или снизу и записываем ее как …10101010С.

Мы можем принять и двухстороннее ограничение, в записи это может выглядеть так: С10101…010101С. В этом случае число ограничено целой частью, косвенно определяет единичный разряд и не включает дробную часть. В любом случае число, образующее числовую цепь, может быть и бесконечно большим. Введение в запись числовой цепи дополнения … 0,0…говорит о том, что число включает и возможную дробную часть после запятой, и дополнительно говорит о направлении увеличения разрядности числа. Мы так и напишем: С1010 …0,00 …С. Ограничение числовой цепи до единичного разряда может быть сделано и таким способом …01010,С.

На числовых цепях удобнее рассматривать процесс переноса и обнуления, т.к. мы рассматриваем динамику этих процессов. Этот процесс не рассматривался ранее отдельно по простой причине — во всех, применяемых сегодня, системах счета этот процесс не является основным. Он рассматривался как необходимая и естественная форма увеличения числа при счете, вместе с процессом заполнения разряда.

Структура числа

Частота заполнения разряда при счете зависит от применяемой системы счета. И здесь уместно ввести понятие структуры числа. Если посмотреть заполнение разрядов какого-либо числа, можно построить какую-то кривую, отражающую это заполнение, изменяющуюся от разряда к разряду. Сразу можно выделить две конечные картинки этой кривой — «нулевое» и «полное» заполнение.

Полученную кривую заполнения разрядов и можно определить как структура числа. А два полярных ее положения, как нулевая и полная структура числа. Эти понятия мы и будем использовать в дальнейшем.

Счет и движение разрядных единиц

С точки зрения математики простейший счет, это — N= 0+1+1+1+1+… — последовательное сложение счетных единиц. Где N и есть число, как результат сложения. Оно меняется с каждой новой единицей. Меняется результат, меняется и его изображение. И так после каждой единицы. Число все время изменяется. Интересно как?

Рис. 15. Движение разрядных единиц от разряда суммирования

Давайте посмотрим на изменение числа в процессе счета. Теперь нас не интересует результат, мы будем смотреть на процесс изменения числа. Вот заполнился один разряд, и единица перепрыгнула в следующий разряд. Вот снова прыгнула…,вот заполнился и другой. Теперь сразу две единицы в разных разрядах перепрыгнули в соседние… и т.д. Если отвлечься от «веса» разрядных единиц, то этот процесс можно назвать движением единиц по разрядам числа. Как на рис.15.

А тем временем, счетные единицы, как палочки в коробку, все поступают и поступают. Процесс счета идет, число изменяется и растет. Все число уже и не определить, … остается следить лишь за частью числа или за числовой цепью.

Вот числовую цепь мы можем определить. Указать количество разрядов в контролируемой цепи, определить разряд, в который и поступают единицы счета, степень влияния на эту цепь разрядов, не попавших в контролируемый участок и т.д. Счет продолжается, … бегут единицы по разрядам числа. Насмотрелись? Остановим счет и подумаем. А что же мы наблюдали? Мы наблюдали динамику изменения числа. Интересовал нас результат? Если честно, то не очень. А изменения числа? Да, интересно. Нас даже не очень интересовало текущее состояние разрядов. Ну, заполняется и ладно. А вот момент обнуления разряда и прыжок единицы интереснее. Кто из нас не ждал момента… 999, … вот сейчас, есть…1000! И чем длиннее это преобразование числа и движение единицы, тем интереснее.…

Оказывается, понимание счета может быть разным.

Рост и развитие числа

Рост числа – направление увеличения числа.

Развитие числа – увеличение его разрядности в направлении движения единиц по разрядам числа. Это увеличение может совпадать с направлением роста, а может и не совпадать.

Во время счета при переполнении разряда сложения мы формируем единицу следующего разряда и передвигаем в следующий, старший разряд. Теперь разберемся с остатком. Если остались целые единицы этого разряда, то оставим их здесь, а если только мелочь, то поищем ей место в подходящих младших разрядах. Нашли подходящий разряд – передвигаем в него остаток, но так чтобы не мешал. А он может, если разряды зависимые. Откуда же мелочь, если складывали только целые единицы? Она появляется, если основание системы счисления не кратно единице. В процессе суммирования счетных единиц эти остатки и образуют второй поток разрядных единиц — в сторону дробной части. Движение разрядных единиц в сторону дробной части числа- это результат иррациональности основания системы счисления.

Таким образом, в рациональных системах счисления есть только одно направление движения единиц, а в иррациональных – два.

В системе счета Бергмана число развивается сразу в двух направлениях. И в сторону увеличения числа, и в сторону расширения его дробной части.

Число – физическая величина.

При таком подходе можно рассматривать число, как величину, имеющую направление увеличения и вектор развития. Число, как переменная величина, получило динамические свойства. Оно может появляться, увеличиваться, расти и развиваться в разных направлениях…

И хотя мы все так же говорим о позиционных системах счисления, положение числа на разрядной оси стало неопределенным. Мы можем говорить лишь о разряде сложения наших счетных единиц, как о постоянной точке в составе числа. И все, пожалуй.

Давайте вспомним такую лесенку — точка, линия, плоскость, объем,… Она имеет к этим трансформациям числа прямое отношение. Все, известные мне сегодня, системы счисления — позиционные. Может быть, существуют и другие, но нас вполне устроят и эти.

Число представляет собой набор разрядов, а каждый разряд формируется по правилам системы счета и представляет собой особый знак — цифру. Цифра в разряде — это число разрядных единиц, попавших в этот разряд в процессе счета, при образовании числа. В формировании числа, разряд, наиболее постоянная величина. Количество единиц в разряде может меняться, а разряд остается. Разрядная шкала — величина постоянная, для любой системы счисления. Число, лишь занимает нужное место на этой шкале. Иногда мы задаем постоянную разрядность чисел, в этом случае все лишние, неиспользованные в формировании числа разряды, мы заполняем нулями. Но это уже тонкости.… Для нас, многоразрядное число — большое! Мы больше себя пугаем, чем даем реальную оценку числу! Длинное — не значит большое, это немного разные вещи.… Давайте не будем рассматривать абсолютную величину числа и будем рассматривать только разрядность числа, как самостоятельную величину, не зависящую от эмоциональных факторов — большое, маленькое.… И примем понятие — длинные числа, не особо утруждая себя учетом реального количества единиц, составляющих его величину. Длина, как физическая величина, должна чем-то измеряться и из чего-то складываться. Уместно, применить геометрические понятия — линия, отрезок, точка... Если задать точке какой-либо размер, то линию вполне уместно измерять и определять точками. В наших рассуждениях длина отрезка линии измеряется количеством размещенных на ней точек. Итак, точка — одноразрядное число или один любой разряд в числе.

Линия- вся шкала разрядов или разрядная ось, какой — либо системы счисления. Это — из «бесконечных»…

Отрезок — число, в нашем обычном понимании, каждая точка которого — разряд.

Если вместо понятия отрезок, использовать понятие вектор, то стрелка показывает направление роста или направление изменения числа. Вектор, даже лучше отражает наши построения. Разрядная ось — натуральный ряд:1;2;3;4;5…- номер разряда числа. Теперь число может быть точно установлено на этой координатной оси. Дальше, формирование системы координат уже не представляет большой трудности. Напомним самим себе, что упомянутая «лесенка», это результат перемещения каждого нового получаемого «объекта», параллельно самому себе в одном из направлений заданной системы координат. Это понятно и естественно. Теперь дело за малым….

Возьмем точку, сделаем из нее отрезок, переместим отрезок и получим плоскость…, и так далее, по лесенке многомерности вверх. Таким образом, число может быть точечным, линейным, плоским, объемным. На таких построениях удобно рассматривать их взаимодействия и его результат в процессе счета.

***