|
Разработана Джорджем Бергманом в 1957 году в США.
Классическая система счисления
Бергмана, кроме традиционного формирования разрядов, использует свойство
степенной функции Ф:
|
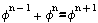
|
(3)
|
Где:
|
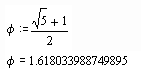
|
(4)
|
Это число Фидия, или «золотое
сечение».
Система Бергмана – полномасштабная
позиционная система счисления с иррациональным основанием Ф. Она позволяет
проводить с числами все арифметические действия в принятом порядке, с
учетом свойств и правил счета этой системы. Складывать, вычитать, умножать
и делить.
Каждое новое значение функции может
быть получено сложением двух предыдущих и, соответственно, единица нового
разряда получается сложением единиц двух предыдущих заполненных разрядов
числа. Основное правило роста разрядности числа 011 =100, т.е. старший
разряд — это сумма двух предыдущих, а не только произведение, как во всех
остальных системах счисления. Основной формой записи числа является запись
единицами старших разрядов 100, а число 011 — эквивалентная, временная
форма записи, которая при окончании операции вычисления должна быть переведена
в основную. Пример: Число 11111, исходя из
основного правила, существовать не может и может рассматриваться только как
временная эквивалентная запись числа перед преобразованием его в нормальную
форму, т.е. 11 111 = 100111 = 101001.
Еще одна особенность: 100+100 =
100+011 = 111= 1001. Вот какие преобразования надо провести, чтобы сложить
два одинаковых числа или единиц в одинаковых разрядах этих чисел. Для
правильного сложения одно из чисел должно быть представлено во временной
эквивалентной форме..011…, как мы делаем при вычитании из пустого разряда в
любой системе счета, занимая единицы из соседнего разряда. Здесь это
постоянная операция и при сложении одинаковых разрядных единиц и при
вычитании из пустого разряда. Давайте посмотрим, как будет выглядеть запись
первых чисел натурального ряда в этой системе счисления:
1= 1
2=10,01=1+1
3=100,01=10,01+1=11,01
4=101,01=100,01+1
5=1000,1001=101,01+1=110,1001=
6=1010,0001= 1000,1001+1=1001,1001
7=10000,0001=1010,0001+1=1011,0001
8=10001,0001=10000,0001+1 и т.д.
Видите, как быстро растет число?
Такое положение возникает в результате того, что десяток не содержит целого
числа единиц, т.к. он меньше 2, и сложение 1+1>Ф, дает следующий разряд
с переполнением. А так как, мы складываем единицы нулевого разряда, у нас
одинаково быстро нарастает как целая часть числа, так и дробная. С другой
стороны, такое быстрое нарастание разрядности может иметь и свои плюсы.
Хорошо отслеживается динамика изменения числа. Каждая новая добавленная
единица вызывает значительные преобразования результата. Часто возникает
симметричность числа. Это видно на примере натурального ряда. Числа
2,3,4,7,8 имеют симметричное отображение относительно запятой, или
относительно первого разряда. Подробнее об этой системе счисления можно
узнать в книгах А.П Стахова,
или на его сайте в Интернете. Там все строго и научно.
Коды Фибоначчи.
Эта система представления числа была
предложена бельгийским врачом Эдуардом Цекендорфом
в 1939 г.,
а теоретическое обоснование у нас она получила в работах А. П. Стахова.
Последовательность Фибоначчи:
1,1,2,3,5,8,13,…
Число Ф здесь присутствует, как
предел отношения соседних членов последовательности. Общая формула этой
последовательности:
Это означает, что каждый новый член
последовательности, это сумма двух предыдущих.
Из последовательности можно сделать
систему счисления. Вот как выглядят в ней первые числа натурального ряда:
1 = 1= 0+1
2 = 10=1+1
3 = 100=10+1=11
4 = 101=100+1
5 = 1000=101+1= 110
6 = 1001=1000+1
7 = 1010=1001+1
8 = 10000=1010+1=1011=1100
9 = 10001=10000+1 и т.д.
Единица старшего разряда в числе –
сумма единиц двух соседних младших разрядов.
А потому число этой системы счета в развернутой
форме не может иметь две единицы подряд в соседних разрядах: 10+1=011=
100. Это основное правило формирования числа в этой системе счета.
Такая система, строго говоря, системой счисления называться не может. Она
не имеет дробной части. Для нее специально разрабатывались правила
умножения и деления. Это система представления числа. Что и отражено в
названии системы – коды Фибоначчи.
Разработка такой счетной системы
вызвана необходимостью. Нужна была система счета, которая бы обладала
свойствами счета Бергмана, но не давала иррациональных и дробных чисел при
переводе в нее целых чисел из другой системы счета. Посмотрите, как
выглядят целые числа натурального ряда в системе Бергмана, и вам сразу
будет понятно, о чем я говорю. Сегодня, на основе кодов Фибоначчи
разработаны новые системы счета.
Даже я приложил к этому руку.
Чуть-чуть. Добавил еще один единичный разряд в позиционное представление
числа. Получились числа с лишним разрядом, если сравнивать с кодами
Фибоначчи. Вот мои основания для этого шага:
Счетная единица, попадая в эту
систему счета, становится десятком, потому что большей счетной образующей у
нас нет. Если рассмотреть любую систему счета, то можно увидеть, что
постоянной величиной является десяток. Он задает систему счета. По количеству
единиц в десятке чаще всего и называют систему счисления: десятичная, двоичная и т.д. А
так как любое число в нулевой степени равно единице, то она и принята за
счетную единицу. Счетные единицы набираются в нулевом разряде числа до его
заполнения и потом образуют основную единицу формирования системы —
десяток. Десяток является постоянным коэффициентом в системе и определяет
пересчет количества счетных единиц в число, сформированное по правилам этой
системы. В нашей системе счета нет другой постоянной величины, кроме
единицы, так как разряды неравномерны и не содержат общего постоянного
множителя для расчета веса единицы следующего разряда. Единица нового
разряда образуется сложением единиц двух предыдущих разрядов. И первый
разряд должен отличаться от единицы, да и нулевой разряд должен быть
выделен. А в нем, в нулевом разряде умещается только одна единица. И в
первом тоже, но переполнения нет. Но единица у нас – десяток. Первая же
счетная единица заполняет нулевой разряд, и переводится в первый разряд, т.е.
в разряд десятков. Так мы это и записываем 0+1=10. Но, мы помним, что
единица первоначально помещается в нулевой разряд, а лишь потом переходит в
первый разряд. Полная запись такая: 00+1=01=10. Если первый разряд уже
заполнен, то следующая единица задержится в нулевом разряде на период
преобразования числа в основную форму записи или на период проведения
счетной операции. А потому: 1 = 10, 2=100, 3= 1000 и т.д.
Но, придуманное мною, никак не
меняет расчеты, а лишь все усложняет и запутывает, хотя и формально верно.
Я бы не стал и вспоминать об этом, если бы не … два единичных разряда. Это
обстоятельство стало отправной точкой геометрического представления числа.
Иррациональная система счисления.
Никаких данных о разработке этой системы
счисления кем-либо у меня нет. Так что, пока это моя вариация на тему.
Нечетные степени числа Ф могут быть
основой системы счисления. Разрядная шкала системы:
Ф(2n+1),…., Ф5,
Ф3, Ф1, Ф-1, Ф-3,
Ф-5,…., Ф-(2n+1)
Как видно, разрядная шкала системы счисления
не содержит разряда счетных единиц – Ф0,
и единица счета не является счетной единицей в этой системе. В этой
системе, представление единицы счета выглядит так: 0,1111111111…
Единицей счета в этой системе
становится Ф, а основанием – Ф2.
Представление числа неоднозначно.
Как и во всех системах счисления с основанием Ф, есть свернутая и
развернутая форма представления числа: 021111…=100000…. Или 02220
… = 10101…
Например: 2,11111… =10,0. Это
вытекает из соотношений:
и
|
Ф2+Ф= (Ф+1)+Ф= 2Ф+1=Ф3
|
(7)
|
Число Ф, это счетная единица для
данной системы счисления и ее основание:
Ф=1,0
2Ф=2,0
3Ф=10,1
4Ф=11,1
5Ф=12,1
6Ф=20,2
7Ф=21,2
8Ф=101,01 и т.д.
Числа натурального ряда 1,2,3,
выглядят гораздо сложнее:
1= 0,111111…
2= 1,01111…
3= 1,2011111…
4= 2,1011111…
5=10,10111111…
Основные правила преобразования
числа в этой системе счисления:
и
такая ситуация возникает при
суммировании разрядной единицы с полным разрядом.
Все правила преобразования
справедливы для всех разрядов числа в этой системе счисления.
И еще:
Это следствие из:
Ф в этой системе, это счетная
единица и умножать на 1 – нормальная операция.
Система счисления обладает
повышенной иррациональностью. Но, с другой стороны, это дает некоторую
свободу в трактовке получаемых чисел.
Пока я не вижу применения такой
системы счета в вычислениях. Она представляет интерес в большей степени, с
философской точки зрения. Все числа этой системы счета иррациональны. Или
по форме записи, или по содержанию.
***
Показанные системы счисления могут
быть применены для вычислений. Но считают они, прямо скажем, не очень. Семь
потов сойдет, пока одно действие закончишь. Для этого дела есть более
привычные и удобные счетные системы.
Но, все относительно. Двоичная
система появилась еще в 19 веке, как курьез. Как абсурд, показывающий
предел упрощения вычислительной системы. Её так и воспринимали до появления
счетных машин.
Область применения этих систем не
вычисления, а контрольные, регистрирующие и сравнительные функции. И
технологические. Проверить, выбрать, сдвинуть, изменить, передать и принять
с наименьшими потерями, … вот для чего эти системы. Для них число не результат
вычислений, а только предмет обработки.
|