Пространственные структуры развития числа.

Теперь попробуем построить пространство развития числа для разных систем счисления. И посмотрим, как в нем будет происходить развитие числа в результате счета.

При счете, сложение как форма математической операции предполагает и геометрический сдвиг при совпадении каких-то условий. Набралось счетных единиц на новую разрядную единицу – сдвигаем. Чем быстрее набирается, тем быстрее идет сдвиг. Счет определяет движение единиц на геометрическом пространстве числа. Скорость движения определяется системой. Чем меньше основание системы, тем быстрее идет движение единиц. Позиционная система представления формализует отображение такого движения. Мы фиксируем точки и шаг перемещения. Не куда попало, а в следующую точку. Позиционное представление системы счисления сделано на предельно сжатом пространстве одномерной оси. Такое представление формирует только одну возможную форму оси – разрядную. Тут вам и шаг перехода, и вес движущейся единицы.

Двоичная система.

Но, если попробовать показать процесс и законы сбора единиц в число в любой системе счета, применяя позиционный принцип, то нам придется использовать плоскость или даже объем. Например, рис.16. Треугольники — это плоскости сложения. В основания этих треугольников попадают счетные единицы, и после заполнения основания — разряда они складываются и формируют единицу старшего разряда в вершине, переходя в следующий разряд уже в виде его разрядной единицы. В принципе, порядок и очередность заполнения не установлен. Заполняется любое свободное место.

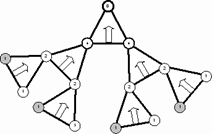
Рис.16. Плоскость сбора двоичного числа. Параллельный сбор.

Видно из чего состоит двоичное число. Сколько и каких разрядов надо заполнить в основании этой пирамиды, чтобы счетные единицы из своих знакомест перекочевали в вершину. И собрались в эквивалентную им одну единицу вершинного разряда.

При введении нового разряда числа необходимо достроить симметричную ветвь такой же пирамиды и поставить новый вершинный разряд.

В основании любого треугольника плоскости сложения два знакоместа. Ну, так и система – двоичная. И все бы хорошо, но в такой системе отображения надо контролировать свободные и уже занятые пути наверх.

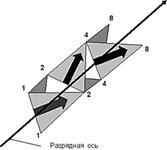
Рис.17. Одномерное двоичное число на разрядной оси. Последовательный сбор.

Чтобы не путаться в путях движения наверх была придумана система последовательного сбора. Она разместилась на одномерной разрядной оси, как на рис.17.

Подобным образом можно построить число в любой рациональной системе счисления. Возрастет лишь количество связей. Количество треугольников плоскостей сложения соответствует основанию системы счисления. Для двоичного счета их два, для десятичной – десять. Все треугольники плоскостей сложения разрядных единиц одного веса выходят из одного основания. Основание треугольника, это и есть разряд — место сбора разрядных единиц.

Заполнились все места основания – следует операция сложения по одной из плоскостей сложения в одно из свободных мест такого же основания следующего разряда. Вроде бы так было всегда. Двигай последовательно единицы по оси, собирай число… или сразу установи его. Тут сложно ошибиться. Порядок строгий. Всё по линеечке…

И, хоть плоскости сложения все равно присутствуют в структуре последовательного сбора двоичного числа позиционного отображения, но мы их как бы «не замечаем». Они остались там, в структуре параллельного сбора. Зато считать стало значительно проще. Заполнилось основание – разряд, ну и двигай новую единицу на любое свободное место в новом разряде. Ось движения одна. Тут не ошибешься и не перепутаешь пути. Вперед и вверх, а там…, и двигали. И в любой системе счисления. Пока не появились машины.

До машинной эры самой распространенной уже была десятичная система. И для машин сразу попробовали применить отработанный десятичный счет. Не тут-то было. Оказалось, что машине трудно объяснить, как это — «на любое свободное…». Не понимает.

Потому и применили двоичную систему. Для ее применения нашлось счастливое свойство. При механизации вычислений второго знакоместа в разряде числа двоичной системы может и не быть. Достаточно одного. Как только оно заполнится, так вторая единица, пришедшая в этот разряд, возвращает этот разряд в нулевое состояние, а сама уходит в следующий, уже с новым весом. Происходит автоматическое суммирование разрядных единиц без самой операции. При таком техническом решении больше одной единицы в разряде быть уже просто не может. Или единица есть или ее нет. И не надо ломать голову, куда разместить вторую счетную единицу, чтобы потом обе сложить, а затем результат сложения перевести в новый разряд.

Решение оказалось настолько удачным, что о первоначальном понимании разряда, как месте сбора единиц просто забыли. Есть 0 и 1. И достаточно. А почему же система – двоичная? Теперь, чаще слышишь ответ: А потому, что 0 и 1. Два состояния.

Даже термин появился – бинарная запись. Это когда только 0 и 1. Число состоит только из этих цифр.

Всё так. Но, система-то так и осталась — двоичная. Значит, заполненный разряд всё же предполагает наличие двух единиц. Хоть на один миг, но – двух. Это отражено и на разрядной оси этой системы: 1;2;4;8; и т.д. Что означает: 2⁰; 2¹; 2²; 2³; и пр.

Разрядная ось определяет принадлежность числа к той или иной системе счисления и позиционную форму его одномерного изображения. Во всех рациональных системах счисления число, полученное последовательным сложением счетных единиц, совпадает с числом, установленным в это пространство на разрядной оси, но не отражает законы получения числа. Это можно увидеть только при построении форм параллельного сбора числа. В общем, или смотри, как устроена система или смотри результат – число. Или – или.

Но для некоторых систем счисления оказалось возможным совместить на одной плоскости и разрядную ось числа, и законы построения системы. И, как следствие таких действий возникли новые свойства числа. Они связаны с появлением пространства числа в координатах разрядных осей. Ведь, даже две координатных оси – это уже плоскость. А если осей много?

Система Бергмана.

Функция:

объединяет значения:

и

В выражении:

Собственно, мы имеем две разных системы счисления, основанных на четных и нечетных значениях степенной функции Ф, связанных соотношением (36). В этих системах счисления соседние разряды числа имеют некоторую независимость, аналогично рациональным системам счисления. Мы строим пространство для системы, основанной на соотношении (33). Она имеет аналогичное построение, но разряды зависимы. Чтобы сохранить независимость разрядов, надо разделить зависимые разряды и разместить их на разные разрядные оси. У нас любой соседний разряд зависим. Значит каждый разряд – на свою ось. Но мы же помним про две разные системы счисления. Учтем и это условие. Сначала устанавливаем параллельные разрядные оси этих систем. Место разрядов определено. Теперь выполняем условие общей системы счисления Бергмана. И начнем устанавливать для этого числа разрядную ось. Соединим все разряды доминантой. Это и есть собственная ось числа. Пространство между осями четных и нечетных разрядов разбилось на осевые треугольники. В каждой вершине разряд. Разряды связаны соотношением (36).

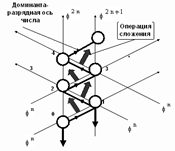
Рис. 18. Пространственная структура числа системы Бергмана.

Полученное пространство развития числа соответствует законам системы Бергмана. Рассмотрим его внимательно. Оно, на рис.18. Координатное пространство можно расширить во все стороны. Справа и слева от показанных осей можно установить новые вертикальные оси, соответственно, четных (34) и нечетных значений функции (35). Здесь мы впервые сталкиваемся с симметричными пространствами развития числа, ограниченными вертикальными осями. Каждый разряд числа принадлежит двум пространствам развития. Сложением единиц в одном разряде мы можем получить два направления увеличения и развития числа.

Установка числа на одну любую разрядную ось Фⁿ приведет к тому, что разряды одного числа окажутся в разных пространствах развития. И дальнейшее изменение этого числа сложением единиц в разряде сложения приведет к фрагментированию числа. Каждый фрагмент числа находится в своем пространстве развития и, соответственно, представляет самостоятельное число.

В этой системе только один нулевой разряд для размещения счетных единиц для двух ветвей числа.

Сложение двух одинаковых разрядных единиц в любом разряде сложения сразу приводит к образованию третьего вектора развития числа. Он направлен вниз от разряда сложения. Образуется дробная часть. Вектор развития дробной части не совпадает с доминантой числа. Это говорит о том, что дробная часть числа в системе Бергмана имеет свои законы развития, не совпадающие с общими законами системы.

Если провести аналогию с элементами построения двоичного счета, то мы видим, что треугольное пространство плоскости переноса и здесь выполняет аналогичную роль. При заполнении основания разрядными единицами идет сложение и перенос новой разрядной единицы в вершину. Только разрядные единицы в его основании – разные.

Система кодов Фибоначчи.

Последовательность Фибоначчи: 1,1,2,3,5,8,13,21,…

Формула получения любого члена последовательности:

В графическом представлении (рис.19.) эта формула выражается стрелкой от основания треугольника. Она и показывает что, суммируя два члена последовательности, находящиеся в основании мы получаем следующий член последовательности в его вершине.

Фигурными стрелками показан сдвиг дробной части при сложении двух единиц одного веса. Он идет по четным или по нечетным разрядам. Как и в системе Бергмана.

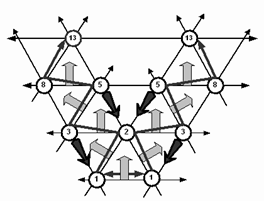
Рис.19. Разрядное пространство числа кодов Фибоначчи.

Такое представление последовательности позволяет увидеть симметричное построение числа, выходящее из одного и того же единичного основания. Уберем вспомогательные оси. Они теперь будут только мешать. И покажем общие направления роста симметричных ветвей числа в системе кодов Фибоначчи. На рис.20. вторая ветвь показана частично. При желании можно восстановить доминанту числа, но стрелки вполне ее заменяют. Направление движения единиц при росте числа видно хорошо.

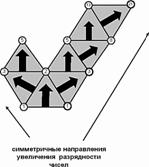
Рис.20. Графическое представление чисел системы кодов Фибоначчи.

Последовательность Фибоначчи – основа кодов Фибоначчи и их разрядная шкала.

Любое число, записанное в кодах Фибоначчи можно установить на этой своеобразной разрядной оси или получить сложением счетных единиц в единичном разряде сложения, общим для обеих ветвей. Числа в кружках указывают вес единиц соответствующего разряда числа. Число может быть установлено или получено сложением счетных единиц, в общем единичном разряде, на любой из ветвей разрядной оси. Только знать бы, в какой ветви мы его получаем?

Давайте посмотрим на рис.21. В данном случае рост разрядности числа идет по правой ветви. Аналогично можно показать рост числа по левой ветви разрядной оси. Для определения правых и левых единиц в цифровой записи может иметь смысл правую единицу в основании разряда записывать как,1. Левую единицу записывать как 1,. Таким образом:,1+1,=10. Запятая в изображении правой и левой единиц основания показывает, с какой стороны от оси симметрии находится единица основания. Это правило можно распространить на форму записи числа на ветви разрядной оси.

Например:,101 (правая)= 101,(левая) = 101 = 4

Теперь можно показать, как идет рост числа в нужную сторону:

,1+1,= 1,1 = 10

10+,1 =,100

,100+,1=,101

,101+1,=,1000

Как мы видим, рост числа идет по правой ветви. Аналогично можно показать рост числа по левой ветви.

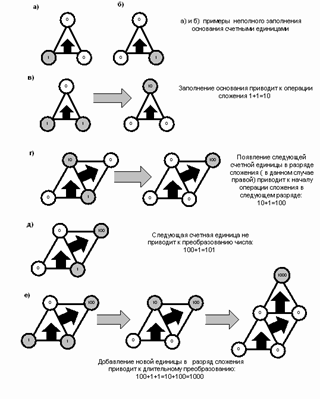
Рис. 21. Рост числа в графическом представлении системы кодов Фибоначчи.

Без построения пространственной структуры развития числа, этих особенностей числа сразу и не увидишь. В принятой позиционной форме записи числа они неуловимы.

Пространство числа систем счисления с использованием в качестве основания взаимообратных чисел.

Теперь уже можно сказать, что система Бергмана формирует треугольное пространство на плоскости. А иррациональная система с основанием Т₂ = 2,4142 и выше, формирует трехмерное пространство в виде тетраэдров. Высота измеряется в 0-мерных точках, и растет с увеличением основания системы. Например, как на рис.22.

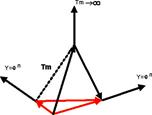
Рис. 22. Образование 3-мерной структуры векторного пространства числа в счетных системах на основе взаимообратных числах.

Ограничение и локализация пространства происходит из-за зависимости соседних узлов -разрядов структуры получаемого числа таких счетных систем.

Например, число в системе Бергмана. Его разряды зависимы, а это требует участия не менее двух точек начала роста векторов развития в реализации роста числа. Следующая фиксируемая точка – их пересечение. Появилось пересечение – пространство ограниченное векторами локализовано. Изменение направления развития уже сформированного пространства никак не отражается на его структуре. Она уже есть.

С ростом основания системы Tm в получаемой плоской структуре появляется третье измерение. Я уже говорил, что, например, система с основанием Т₂ = 2,4142 уже формирует объем.

Единичная система.

Как мы видим на рис.23., положительные и отрицательные степени основания имеют одно абсолютную величину, равную 1. Степени отрицательного основания имеют знакопеременную характеристику.

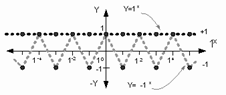
Рис.23. Геометрическое представление значений функций Y=1^x и Y=-1^x.

Количественное наполнение чисел (рис.24.) полной структуры растет равномерно и одновременно с ростом разрядности. Таким качеством обладает только эта система счисления.

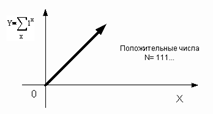
Рис.24. Количественное наполнение положительных чисел в единичной системе счисления.

Если сравнить рис.24. и рис.25., то можно видеть зеркальную симметрию ветвей оценки количественного наполнения положительных целых и дробных чисел. Видимо, это можно использовать в вычислительной технике. В единичной системе счисления любое число, как целое, так и с десятичной дробью может содержать только целое количество счетных единиц.

Целая и дробная ветви разрядов положительного числа единичной системы симметричны относительно оси Y. Это связывает единичную систему счисления с системами на основе числа Ф.

Наиболее близка к единичной, система кодов Фибоначчи. Она также имеет две независимые ветви развития числа, расходящиеся из одной точки.

Таким образом, число в единичной системе счисления может развиваться в двух симметричных направлениях относительно точки суммирования в нулевом разряде числа.

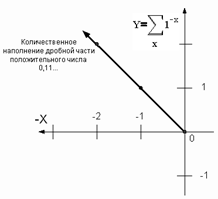
Рис. 25. Количественное наполнение дробной части положительных чисел единичной системы счисления.

Единичная система счисления имеет смысл, видимо, только для нужд вычислительной техники и коммутации. Это изначально искусственная система. Она так и разрабатывалась. Искусственно введенная малая величина q, предназначенная только для существования этой системы вдруг оказалась ключом к продвижению единичного импульса в длинной цепи однотипных элементов, обозначающих очередной разряд какого-то числа. Смысл управления сводится к операции умножения на 1¹. В единичной системе выражение:

имеет смысл. Введением множителя мы и можем сделать разрядный сдвиг, как всего числа, так и его части в любую сторону. Или провести одну единицу по всей линии разрядов числа. Все зависит от нашего желания и технической необходимости. Посмотрите на рис.26., сколько вариантов такого продвижения. И это еще не все.

Давайте рассмотрим эти несколько вариантов. В варианте А) мы загружаем единицу со входа в первый разряд. Добавление величины q по линии сдвига эквивалентно умножению на 1¹. И наша единица переходит в следующий разряд. Снова добавляем q и снова – сдвиг. Так до конца линейки сдвига.

Вариант Б) отличается только стороной управления.

Вариант В) показывает, как можно делать сдвиг в обе стороны от разряда загрузки.

Вариант Г) показывает возможность независимого умножения в разных разрядах одного числа. Таким образом можно изменять число.

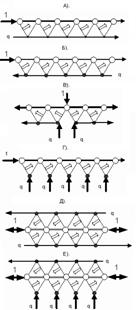
Рис.26. Варианты продвижения разрядных единиц в числе единичной системы счисления.

Варианты Д) и Е) – комбинированное управление движением единиц по разрядной оси. Они допускают как умножение числа, так и деление на 1¹. Как общее, так и разрядное. Загружаем с одной стороны, а получаем с другой. Движение двухстороннее. Потом мы увидим и техническую реализацию этого процесса. И цель ее применения.

Оказывается, она очень практичная, эта надуманная единичная система.

***